Aztec Crash Course
First step towards Aztec 3.0
February 2023
UTXO and Account Models
UTXO Model















Recap

- Zero Knowledge Proof using 3-colourable graph
- Password management

- Use of encryption and hashing in Aztec
Plaintext
Encryption \((\text{AES})\)
Hashing \((\text{SHA-}256)\)



Groups
- \(\textcolor{pink}{\text{Associativity}}\): For any \(G_1, G_2, G_3 \in \mathbb{G}\)
- \(G_1 + (G_2 + G_3) = (G_1 + G_2) + G_3\)
-
\(\textcolor{lightblue}{\text{Identity}}\): There exists \(\mathcal{O} \in \mathbb{G}\) such that for any \(G \in \mathbb{G}\)
- \(\mathcal{O} + G = G + \mathcal{O} = G\)
-
\(\textcolor{orange}{\text{Inverse}}\): For every \(G \in \mathbb{G}\), there exists \(I \in \mathbb{G}\) such that:
- \(I + G = G + I = \mathcal{O}\)
Binary operation
A set of elements \(\{G_1, G_2, \dots\}\)
Groups
\(\textcolor{pink}{\text{Associativity}}\) \(\hspace{1.5cm}\textcolor{lightblue}{\text{Identity}}\) \(\hspace{1.5cm}\textcolor{orange}{\text{Inverse}}\)
\(=\{0, 1, 2, \dots, 7\}\)
\(\text{ mod }8\)
\(0\)
\(1\)
\(2\)
\(6\)
\(4\)
\(3\)
\(5\)
\(7\)
\(1+(2+4) = \)
Groups
\(\textcolor{pink}{\text{Associativity}}\) \(\hspace{1.5cm}\textcolor{lightblue}{\text{Identity}}\) \(\hspace{1.5cm}\textcolor{orange}{\text{Inverse}}\)
\(=\{0, 1, 2, \dots, 7\}\)
\(\text{ mod }8\)
\(0\)
\(1\)
\(2\)
\(6\)
\(4\)
\(3\)
\(5\)
\(7\)
\(1+(2+4) = \)
Groups
\(\textcolor{pink}{\text{Associativity}}\) \(\hspace{1.5cm}\textcolor{lightblue}{\text{Identity}}\) \(\hspace{1.5cm}\textcolor{orange}{\text{Inverse}}\)
\(=\{0, 1, 2, \dots, 7\}\)
\(\text{ mod }8\)
\(0\)
\(1\)
\(2\)
\(6\)
\(4\)
\(3\)
\(5\)
\(7\)
\(1+(2+4) = \)
\(7\)
\(=(1+2)+4\)
Groups
\(\textcolor{pink}{\text{Associativity}}\) \(\hspace{1.5cm}\textcolor{lightblue}{\text{Identity}}\) \(\hspace{1.5cm}\textcolor{orange}{\text{Inverse}}\)
\(=\{0, 1, 2, \dots, 7\}\)
\(\text{ mod }8\)
\(0\)
\(1\)
\(2\)
\(6\)
\(4\)
\(3\)
\(5\)
\(7\)
\(1+(2+4) = \)
\(7\)
\(=(1+2)+4\)
\(4+0 = 0 + 4 = 4\)
Groups
\(\textcolor{pink}{\text{Associativity}}\) \(\hspace{1.5cm}\textcolor{lightblue}{\text{Identity}}\) \(\hspace{1.5cm}\textcolor{orange}{\text{Inverse}}\)
\(=\{0, 1, 2, \dots, 7\}\)
\(\text{ mod }8\)
\(0\)
\(1\)
\(2\)
\(6\)
\(4\)
\(3\)
\(5\)
\(7\)
\(1+(2+4) = \)
\(7\)
\(=(1+2)+4\)
\(4+0 = 0 + 4 = 4\)
\((3 + x) \text{ mod }8 = 0\)
Groups
\(\textcolor{pink}{\text{Associativity}}\) \(\hspace{1.5cm}\textcolor{lightblue}{\text{Identity}}\) \(\hspace{1.5cm}\textcolor{orange}{\text{Inverse}}\)
\(=\{0, 1, 2, \dots, 7\}\)
\(\text{ mod }8\)
\(0\)
\(1\)
\(2\)
\(6\)
\(4\)
\(3\)
\(5\)
\(7\)
\(1+(2+4) = \)
\(7\)
\(=(1+2)+4\)
\(4+0 = 0 + 4 = 4\)
\((3 + x) \text{ mod }8 = 0\)
\(\implies x =5\)
Groups
- Finite groups: finite number of elements
- Order of the group: the size of the set (Prev example \(|\mathbb{G}|=8\))
- Cyclic groups: given a generator \(G \in \mathbb{G}\)
\(\mathbb{G}=\{G, 2G, 3G, 4G, \dots\}\)
- In the previous example, \(G=1\)
- For a prime ordered group, every non-zero element is a generator!
\(\mathbb{G}=\{0, 1, 2,3,4\}\)
\(1\)
\(2\)
\(3\)
\(4\)
\(G\)
\(2G\)
\(3G\)
\(4G\)
\(5G\)
\(2\)
\(3\)
\(4\)
\(0\)
\(0\)
\(4\)
\(1\)
\(3\)
\(0\)
\(4\)
\(1\)
\(2\)
\(2\)
\(0\)
\(1\)
\(3\)
Elliptic Curves over Reals
- The set \(E\) of real solutions \((x,y)\) of the equation
- \(E\) also includes the "point at infinity": \(\mathcal{O}\). Also, \(4a^3 + 27b^2 \neq 0.\)
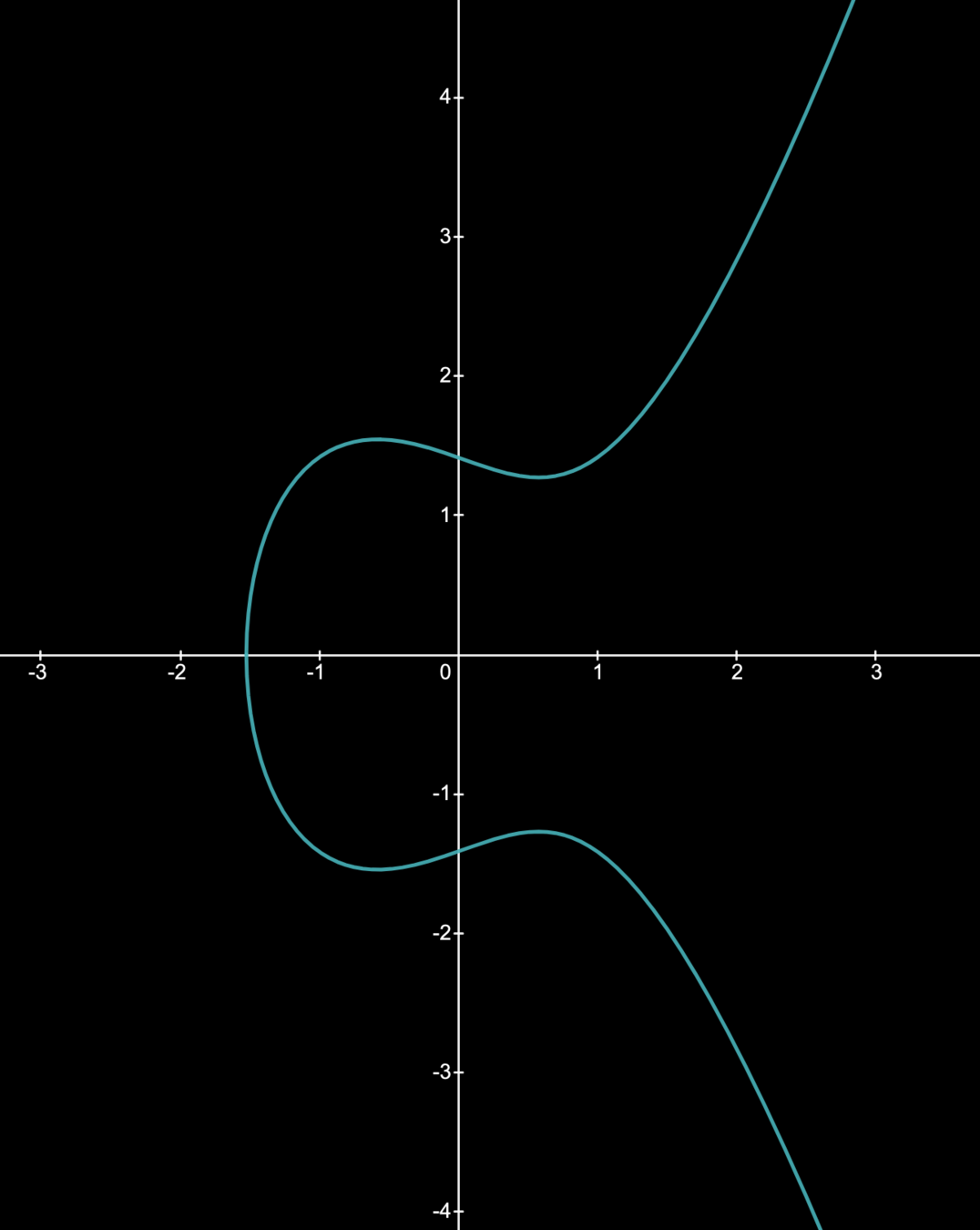
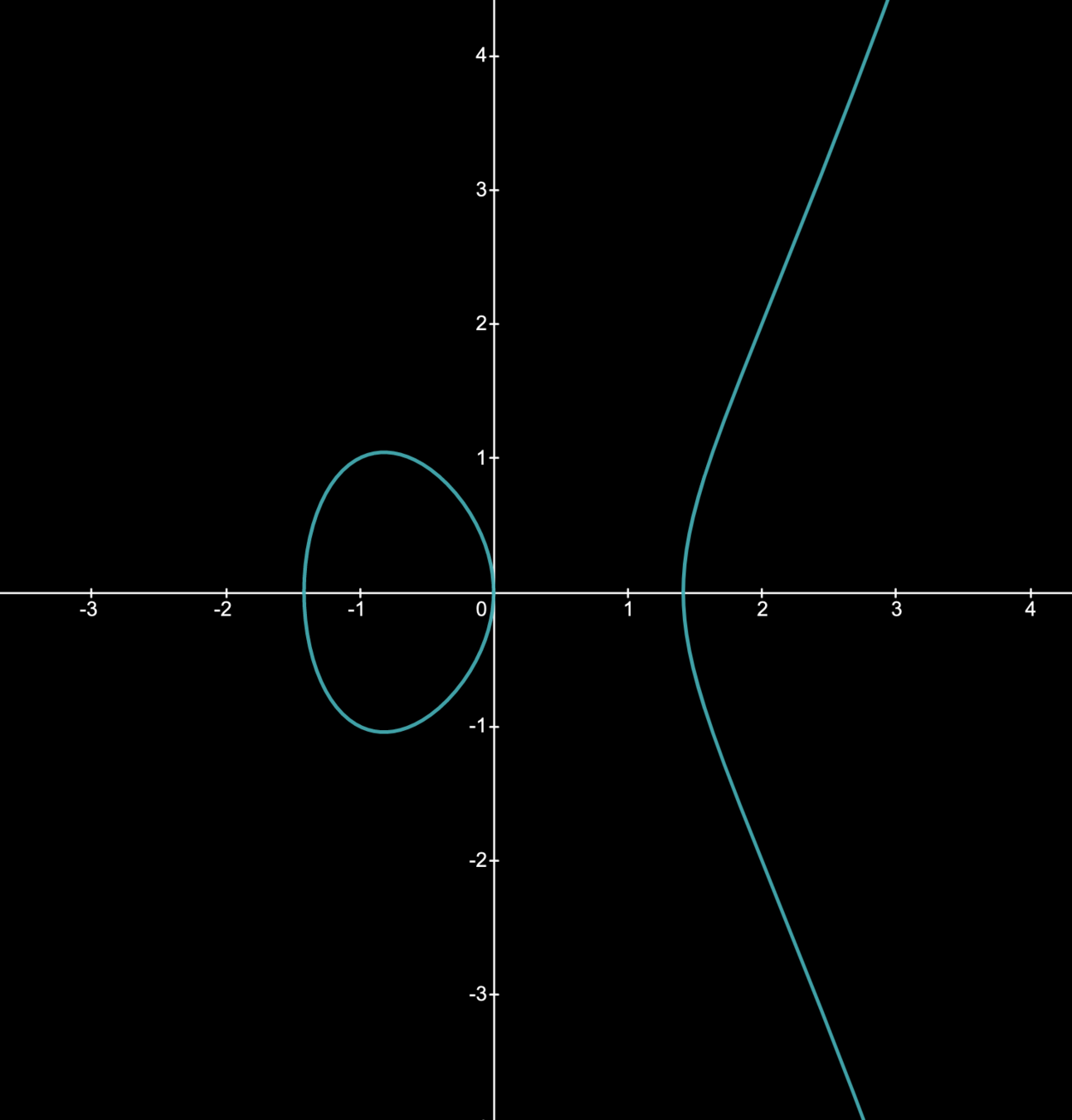
\(y^{2}=x^{3}-2x\)
\(y^{2\ }=x^{3}-x+2\)
Point Addition
Fields
Addition operator
A set of elements \(\{f_1, f_2, \dots\}\)
Multiplication operator
- \(\mathbb{F}\) is an Abelian group under \(+\) with identity \(\mathcal{O}_{+}=0\)
- \(\mathbb{F} \setminus \{0\}\) is an Abelian group under \(*\) with identity \(\mathcal{O}_{*}=1\)
- \(\mathbb{F}\) is distributive, i.e. for any \(a,b,c\in \mathbb{F}\)
\(a * (b+c) = a*b \ + \ a*c\)
- A finite field has a finite size!
Prime Field
- A field \(\mathbb{F}\) with a prime order is a prime field
- Example: \(\mathbb{F}_p := \{0, 1, 2, 3, \dots, p-1\}\) for a prime \(p\)
- \(+\) and \(*\) are defined as
\(x + y = (x+y) \text{ mod }p\)
\(x * y = (xy) \text{ mod }p\)
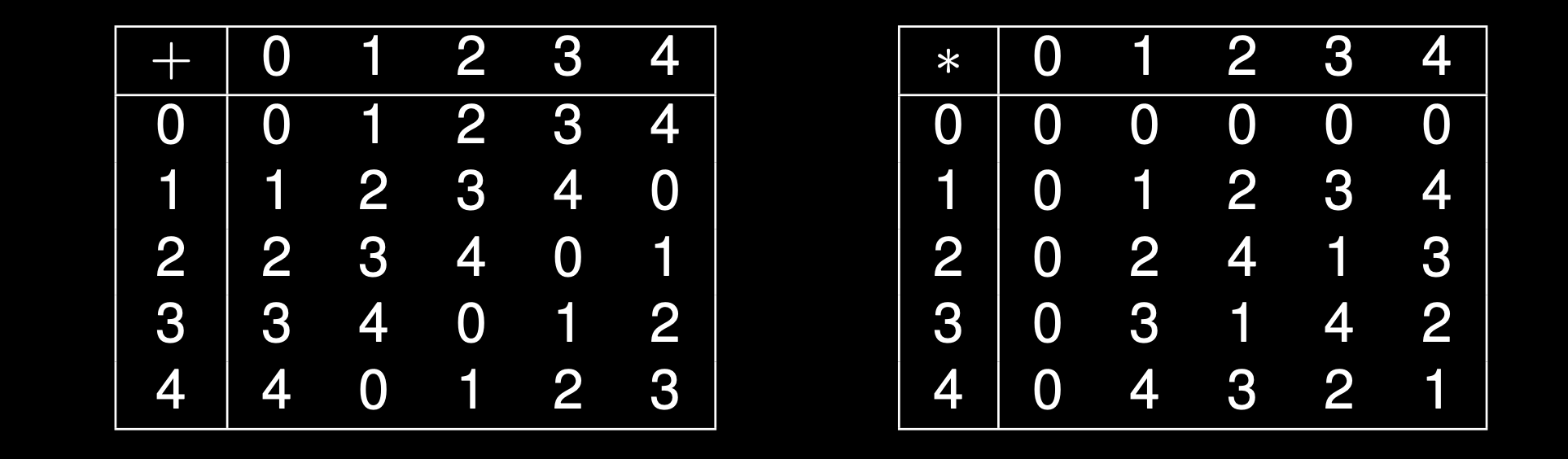
- In a field, division is done as: \(\frac{a}{b} = a * b^{-1}\)
Elliptic Curves over Finite Fields
- The set \(E\) of solutions \((x,y)\in \mathbb{F}^2\) of the equation
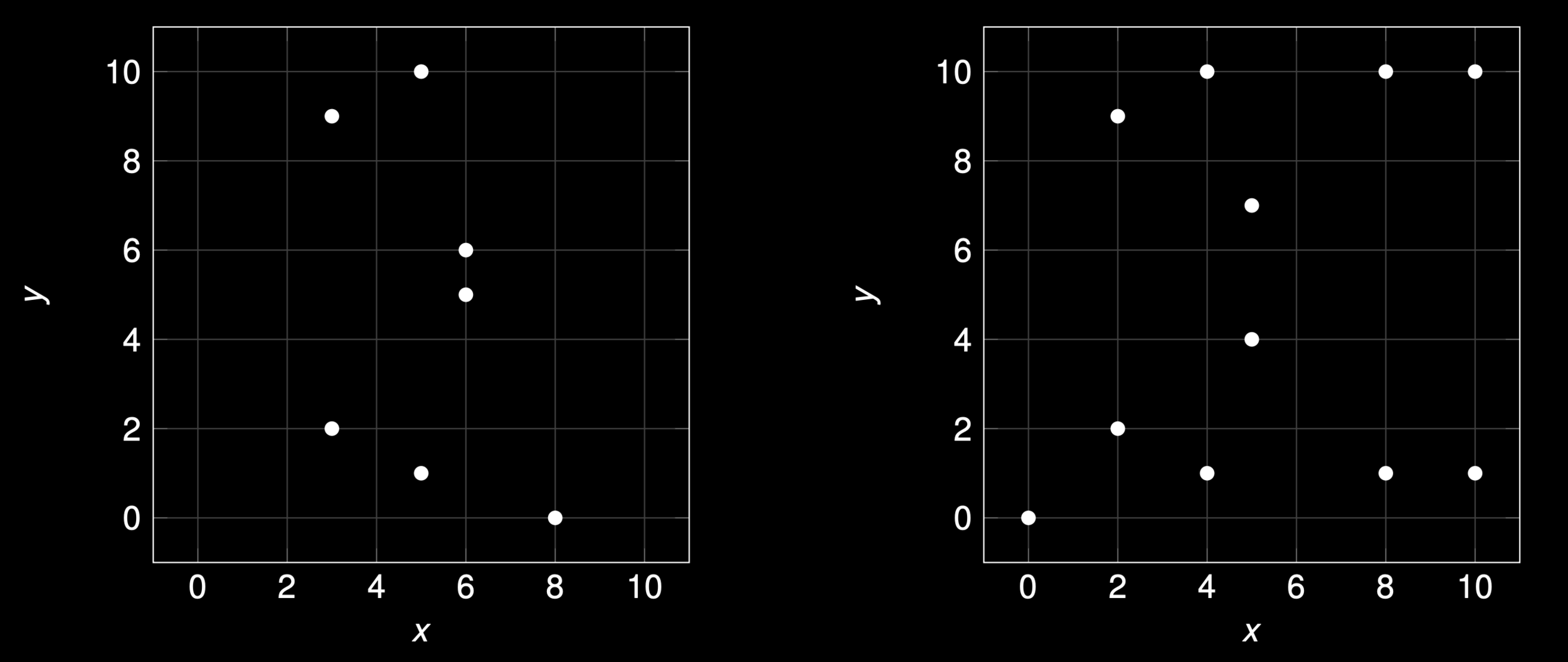
\(y^2 = x^3+10x+2\) over \(\mathbb{F}_{11}\)

\(y^2 = x^3+9x\) over \(\mathbb{F}_{11}\)
Point Addition over \(\mathbb{F}_p\)

\(y^2 = x^3+10x+2\) over \(\mathbb{F}_{11}\)
\((3,2) + (6,5) = \)
\((3,9)\)
Point Addition over \(\mathbb{F}_p\)

\(y^2 = x^3+10x+2\) over \(\mathbb{F}_{11}\)
\((3,2) + (6,5) = \)
\((3,9)\)
\((3,9)+(5,10) = \)
\((6,6)\)
Bitcoin's EC: \(\texttt{secp256k1}\)
- \(y^2=x^3+7\) over \((x,y)\in \mathbb{F}_p^2\) where
\(n =\texttt{FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141}\)
- The set \(E \cup \{\mathcal{O}\}\) is of size
- A private key is \(s \in \{1, 2, 3, \dots, n-1\}\)
- Public key is \(sP = \underbrace{P+P+\dots+P}_{s\text{ times}}\) where \(P \in E\) is group generator

\(P:\)
Summary
- Simple examples of ECC basic
- Groups, prime-ordered groups
- Fields, prime-ordered fields
- Elliptic curve over Reals
- Elliptic curve over finite fields
- Real-life numbers for Bitcoin's elliptic curve
- In the next discussion:
- Schnorr signatures
- Discrete Log Problem
- How hard is it to break ECC?