Aztec 2.0 \(\rightarrow\) Aztec Connect
A
Z
T
E
C
A
Z
T
E
C
nonymous
ero-knowledge
ransactions
fficient
ommunication
with






A Join-Split Transaction
A
Z
T
E
C
nonymous
ero-knowledge
ransactions
fficient
ommunication
with






A Join-Split Transaction




Storage
Offchain Data






Sent to Bob offline
Encryption key
Decryption key
Synchronisation







Recap: Hash Functions
\(\texttt{Input}\)
\(\texttt{Output}\)
\(\texttt{SHA3 }(\text{Keccak})\)
- Hash functions have three properties
- Fast to compute: \(y = H(x)\)
- Collision resistance: \(H(x) = H(x') {\ \;\not\!\!\!\implies \ } x \neq x'\)
- Pre-image resistance: \(y = H(x) {\ \;\not\!\!\!\implies \ } x\)
- A modern GPU can compute \(\approx 29\times 10^7\) hashes per second
- We must not use fast hash functions for password hashing
\(\text{SHA-}3(\hspace{2cm}) = \Big(\hspace{4.8cm}\Big)\)
\(\texttt{b27ensk=wh}\)
\(\texttt{b654e400924d2d43b0b49b6beb52cd96}\)
\(\texttt{c983e26536eb455f80e2ab7fe07827a8}\)
\(\texttt{2bd0650eae8e3e9bda13c067f08da778}\)
\(\texttt{9624f52e63757ce0db5da6940c0c74e1}\)
\(\texttt{tbsowsn293nsj}\)
\(\texttt{089f29913f16c3cea73116b3445d2244}\)
\(\texttt{97fea922c4c501f1cd965cfd921c1a4d}\)
\(\texttt{92528721816}\)
- So why do we need hash functions in Aztec?
- Compact representation of variable-length data
Recap: Hash Functions
Merkle Trees
- Note commitments are stored in \(\mathbb{D}\) while spent note nullifiers in \(\mathbb{N}\)
- Suppose we want to store \(2^{k}\) files in a decentralized and succinct way








\(f_1\)
\(f_2\)
\(f_3\)
\(f_4\)
\(f_5\)
\(f_6\)
\(f_7\)
\(f_8\)
\(H(f_1)\)
\(H(f_2)\)
\(H(f_3)\)
\(H(f_4)\)
\(H(f_5)\)
\(H(f_6)\)
\(H(f_7)\)
\(H(f_8)\)
Merkle Trees
- Note commitments are stored in \(\mathbb{D}\) while spent note nullifiers in \(\mathbb{N}\)
- Suppose we want to store \(2^{k}\) files in a decentralized and succinct way
\(H(f_1)\)
\(H(f_2)\)
\(H(f_3)\)
\(H(f_4)\)
\(H(f_5)\)
\(H(f_6)\)
\(H(f_7)\)
\(H(f_8)\)
\(H'(H(f_1), H(f_2))\)
\(H'(H(f_3), H(f_4))\)
\(H'(H(f_5), H(f_6))\)
\(H'(H(f_7), H(f_8))\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\(h^3_1\)
\(H'(h^1_1, h^1_2)\)
\(H'(h^1_3, h^1_4)\)
\(H'(h^2_1, h^2_2)\)
Merkle Trees
\(H(f_1)\)
\(H(f_2)\)
\(H(f_3)\)
\(H(f_4)\)
\(H(f_5)\)
\(H(f_6)\)
\(H(f_7)\)
\(H(f_8)\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\(h^3_1\)
- Indeed, \(h_1^3\) is succinct form of the files. How do we prove inclusion?














Merkle Trees
- Indeed, \(h_1^3\) is succinct form of the files. How do we prove inclusion?
- Only \(\left( H(f_6), h^1_4, h_1^2 \right)\) are enough to prove inclusion of \(f_5\)! Sister nodes!
\(H(f_1)\)
\(H(f_2)\)
\(H(f_3)\)
\(H(f_4)\)
\(H(f_5)\)
\(H(f_6)\)
\(H(f_7)\)
\(H(f_8)\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\(h^3_1\)

















Merkle Trees
- For root \(h_1^{3}\), index \(\text{idx} = 5\), the Merkle proof is \(\left\{H(f_6), h_4^1, h_1^2\right\}\).
\(H(f_1)\)
\(H(f_2)\)
\(H(f_3)\)
\(H(f_4)\)
\(H(f_5)\)
\(H(f_6)\)
\(H(f_7)\)
\(H(f_8)\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\(h^3_1\)

















Data Tree
- \(\mathbb{D}\) is size \(2^{32}\) insert-only Merkle tree which supports batch updates
- Contains commitments to all account and value notes ever created in Aztec

Data Tree
- \(\mathbb{D}\) is size \(2^{32}\) insert-only Merkle tree which supports batch updates
- Contains commitments to all account and value notes ever created in Aztec
- Suppose we wish to add \(\mathcal{A}_1, \mathcal{A}_2, \mathcal{V}_1, \mathcal{V}_2\) to \(\mathbb{D}\)
Data Tree
- Old data root: \(D_{\text{old}},\)
\(\mathbb{C}(\mathcal{A}_1)\)
\(\mathbb{C}(\mathcal{A}_2)\)
\(\mathbb{C}(\mathcal{V}_1)\)
\(\mathbb{C}(\mathcal{V}_2)\)
\(D\)
New data root: \(D_{\text{new}}\)
Data Tree
- Old data root: \(D_{\text{old}},\)
- With subtree root \(S\) and the partial proof \(\{h_1, h_2\}\), we can verify:
\(\mathfrak{C}(\mathcal{A}_1)\)
\(\mathfrak{C}(\mathcal{A}_2)\)
\(\mathfrak{C}(\mathcal{V}_1)\)
\(\mathfrak{C}(\mathcal{V}_2)\)
\(D\)
New data root: \(D_{\text{new}}\)
\(S\)
\(h_1\)
\(h_2\)
\(D_{\text{new}} \stackrel{?}{=} H\left(h_2, H(S, h_1)\right)\)
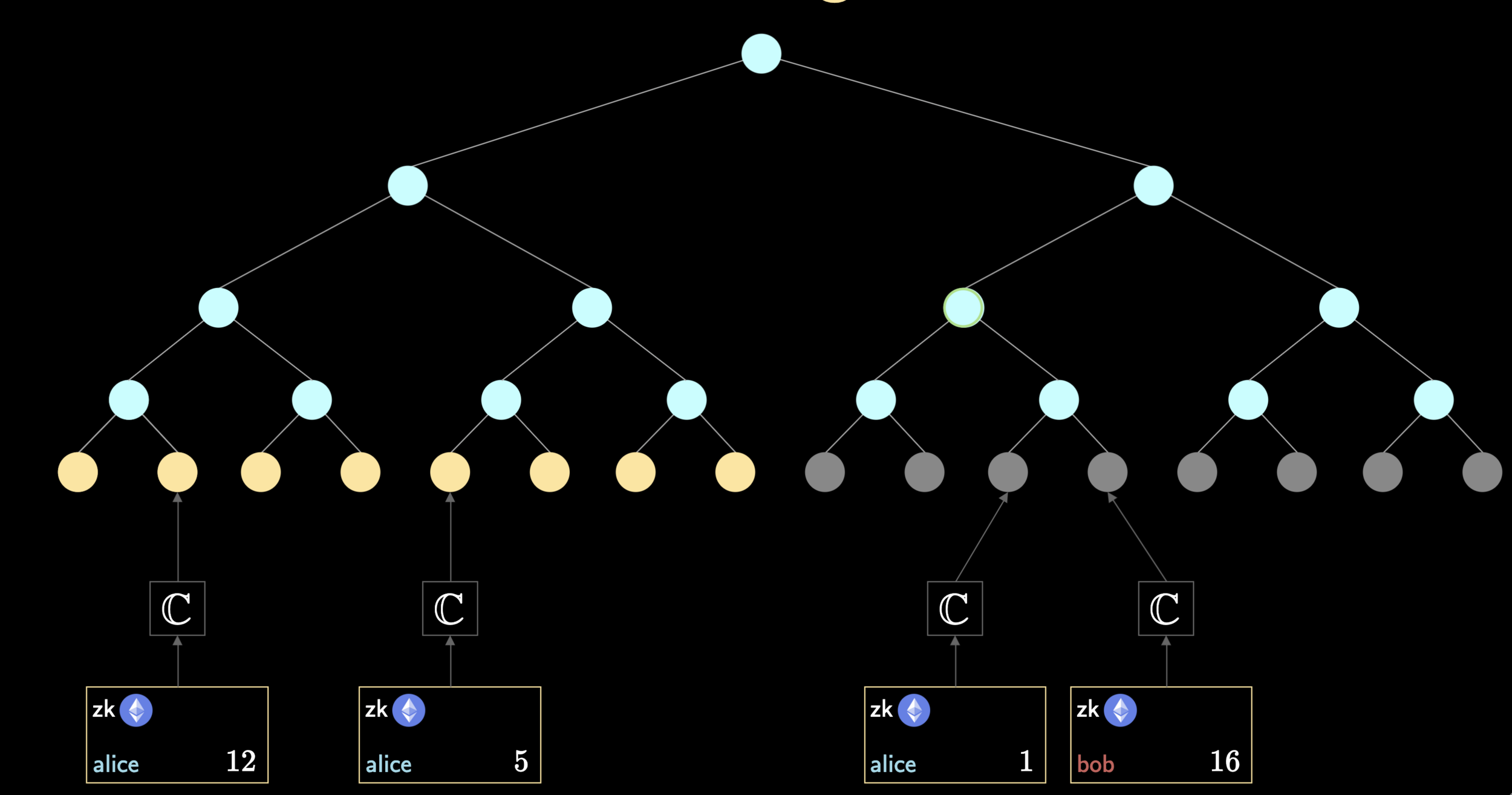
Nullifier Tree
- \(\mathbb{N}\) is size \(2^{256}\) sparse Merkle tree which supports non-membership proofs
- To prove that a note is unspent, we need to give a non-membership proof
- Suppose we have \(16\) leaf values \(\{A, B, \dots, P\}\) s.t. \(\text{idx}(A) = 1\) and so on
- To prove \(J \notin \mathbb{T}\), a membership proof \((10, \phi, \pi_{\text{merkle}})\) suffices!
\(A\)
\(F\)
\(N\)
\(\phi\)
Nullifier Tree
- \(\mathbb{N}\) is size \(2^{256}\) sparse Merkle tree which supports non-membership proofs
- To prove that a note is unspent, we need to give a non-membership proof
- A nullifier of a note is a computed as
\(A\)
\(F\)
\(N\)
\(\phi\)
\(\mathbb{N}(\mathcal{V}) = \textsf{hash}\left( \mathbb{C}(\mathcal{V})_x, \ \text{idx} \right) \in \mathbb{F}_q, \ q \approx 2^{254}\)
Join-Split Circuit
UTXO vs Account
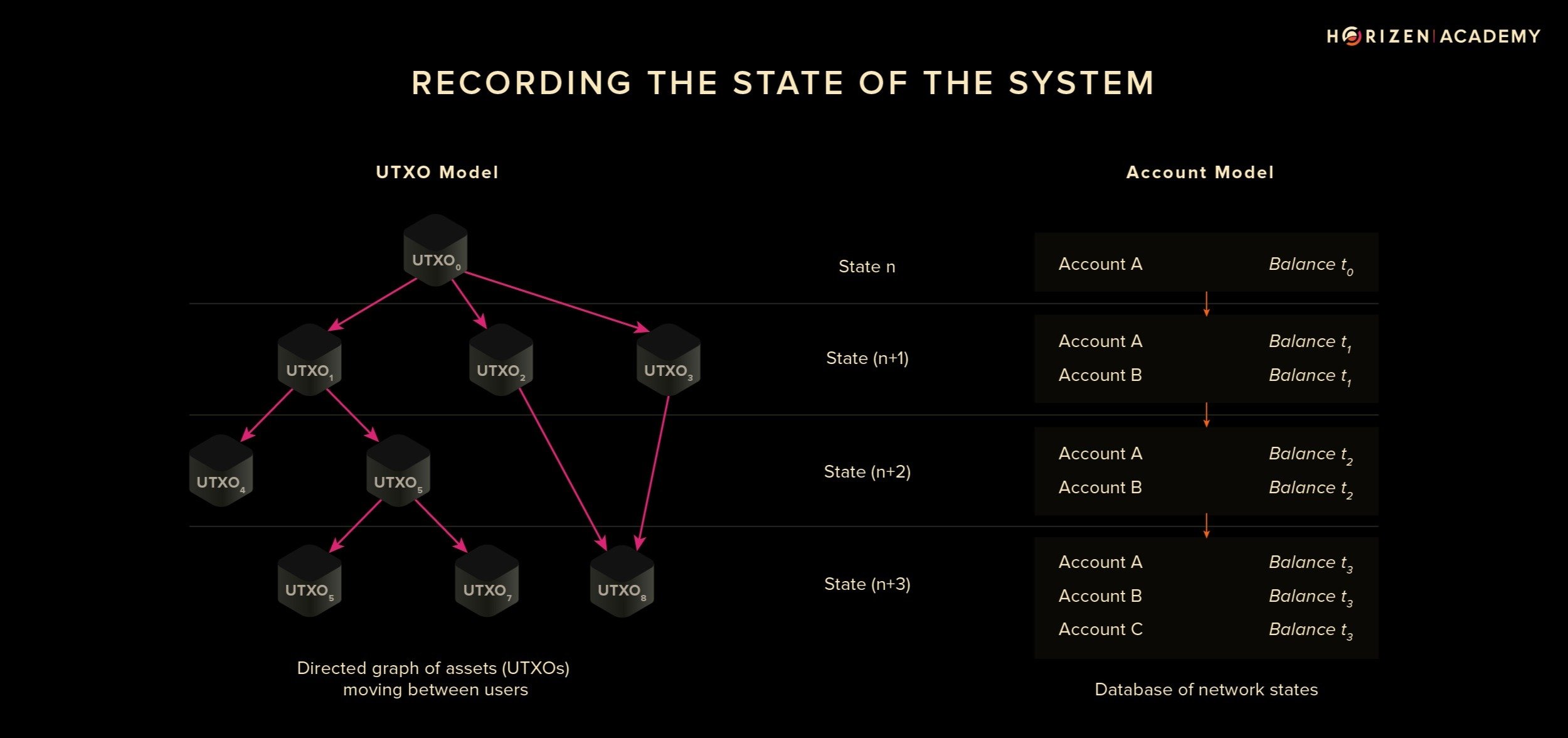
Aztec 2.0

20

Bob

Alice
Open account

\(\texttt{bob}\)

\(\texttt{alice}\)

8


2



10


10

0.5


1.5



18


2
10

Shield
Rollup Contract


Account UTXO
Value UTXO
Private sends
\(\text{zkETH}=8.5\)
\(\text{zkDAI}=18\)
\(\text{zkETH}=1.5\)
\(\text{zkDAI}=2\)
Withdraw
\(0\)
1.5

Join-Split Transaction


10


10


18


1

Alice

Bob
- Alice is the owner of those notes
- Alice's account key is correct
- Alice's notes (i.e. commitments \(\mathbb{C}(I_1), \mathbb{C}(I_2)\)) are present in the data tree
- If so, compute the nullifier values \(\mathbb{N}(I_1), \mathbb{N}(I_2)\) of Alice's notes
- Compute transaction fee: \(f = (10 + 10) - (18 + 1) = 1\)
- Verify the signature signed by Alice over the transaction data
- Output: \(\mathbb{C}(O_1), \mathbb{C}(O_2), \mathbb{N}(I_1), \mathbb{N}(I_2), f \)
Transaction Chaining

Alice


10


2


2


2


2


2
Transaction Chaining

Alice


10


2


0


2


2


2


2


8


0


6


0


4


0
Total wait time: \(2\) hours
Transaction Chaining

Alice


10


2


0


2


2


2


2


8


0


6


0


4


0



- The chained notes are not added to the data tree
- Hence, they don't need a merkle membership check
- Submit these 4 "chained" transactions in the same rollup block
Value Notes
- Aztec uses notes as a basis for private transactions on Ethereum

Value
Asset id

Owner
Secret
\(a \ \in \ \mathbb{Z}_2^{32}\)
\(A \ \in \ \mathbb{G}_1\)
\(v \ \in \ \mathbb{F}_q\)
\(s \ \in \ \mathbb{F}_q\)
- A value note is given as: \(\mathcal{V} = \{a, v, \mathcal{O}, s\}\)
- A note incorporates the on-chain identity (i.e. account PK) of its owner
- The secret \(s\) is the hiding factor in computing Pedersen commitment to a note: