ECCVM
Why, What and How?
Plonk Verification
e(P_{\textsf{left}}, [x]_2) \stackrel{?}{=} e(P_{\textsf{right}}, [1]_2)
P_{\textsf{left}} = \textcolor{olive}{1}\cdot \textcolor{orange}{[W_1]} + \textcolor{olive}{u}\cdot \textcolor{orange}{[W_2]}
\begin{aligned}
P_{\textsf{right}} =&\ \textcolor{olive}{\mathfrak{z}}\cdot \textcolor{orange}{[W_1]} +
\textcolor{olive}{u\mathfrak{z}\omega}\cdot \textcolor{orange}{[W_2]} +
\textcolor{olive}{s}\cdot \textcolor{brown}{[1]}
\ + \\[3pt]
&\ \textcolor{olive}{v}\cdot \textcolor{orange}{[a]} +
\textcolor{olive}{v^2}\cdot \textcolor{orange}{[b]} +
\textcolor{olive}{v^3}\cdot \textcolor{orange}{[c]} +
\textcolor{olive}{v^4}\cdot \textcolor{brown}{[s_{\sigma_1}]} +
\textcolor{olive}{v^5}\cdot \textcolor{brown}{[s_{\sigma_2}]}
\ + \\[3pt]
&\ \textcolor{olive}{\bar{a}\bar{b}}\cdot \textcolor{brown}{[q_m]} +
\textcolor{olive}{\bar{a}}\cdot \textcolor{brown}{[q_l]} +
\textcolor{olive}{\bar{b}}\cdot \textcolor{brown}{[q_r]} +
\textcolor{olive}{\bar{c}}\cdot \textcolor{brown}{[q_o]} +
\textcolor{olive}{1}\cdot \textcolor{brown}{[q_c]}
\ + \\[3pt]
&\ \textcolor{olive}{s_2}\cdot \textcolor{orange}{[z]} +
\textcolor{olive}{s_3}\cdot \textcolor{brown}{[s_{\sigma_3}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}}\cdot \textcolor{orange}{[t_{lo}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^n}\cdot \textcolor{orange}{[t_{mid}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^{2n}}\cdot \textcolor{orange}{[t_{hi}]}
\end{aligned}
Pre-computed
Proof
- Two variable-base MSMs with constant sizes
Recursive Verification
e(P_{\textsf{left}}, [x]_2) \stackrel{?}{=} e(P_{\textsf{right}}, [1]_2)
e(P^{\textcolor{red}{1}}_{\textsf{left}}, [x]_2) \stackrel{?}{=} e(P^{\textcolor{red}{1}}_{\textsf{right}}, [1]_2)
e(P^{\textcolor{red}{2}}_{\textsf{left}}, [x]_2) \stackrel{?}{=} e(P^{\textcolor{red}{2}}_{\textsf{right}}, [1]_2)
e(P^{\textcolor{red}{m}}_{\textsf{left}}, [x]_2) \stackrel{?}{=} e(P^{\textcolor{red}{m}}_{\textsf{right}}, [1]_2)
\vdots
e(P_{\textsf{left}} + \textcolor{grey}{v}P^{\textcolor{red}{1}}_{\textsf{left}} + \dots + \textcolor{grey}{v^m}P^{\textcolor{red}{m}}_{\textsf{left}}, [x]_2) \stackrel{?}{=} e(P_{\textsf{right}} + \textcolor{grey}{v}P^{\textcolor{red}{1}}_{\textsf{right}} + \dots + \textcolor{grey}{v^m}P^{\textcolor{red}{m}}_{\textsf{right}}, [1]_2)
Recursive Verification
e(P_{\textsf{left}} + \textcolor{grey}{v}P^{\textcolor{red}{1}}_{\textsf{left}} + \dots + \textcolor{grey}{v^m}P^{\textcolor{red}{m}}_{\textsf{left}}, [x]_2) \stackrel{?}{=} e(P_{\textsf{right}} + \textcolor{grey}{v}P^{\textcolor{red}{1}}_{\textsf{right}} + \dots + \textcolor{grey}{v^m}P^{\textcolor{red}{m}}_{\textsf{right}}, [1]_2)
- Aggregate proof verification by:
- Compute \(P^i_{\textsf{left}}, P^i_{\textsf{right}}\) for \(i\)-th proof
- Accumulate them in the overall \(P_{\textsf{left}}\) and \(P_{\textsf{right}}\)
P_{\textsf{left}} \leftarrow P_{\textsf{left}} + \textcolor{grey}{v^i}P^{\textcolor{red}{i}}_{\textsf{left}}
P_{\textsf{right}} \leftarrow P_{\textsf{right}} + \textcolor{grey}{v^i}P^{\textcolor{red}{i}}_{\textsf{right}}
- We can perform this computation in a Plonkish circuit
- This circuit will "recursively verifiy" a given Plonk proof
- Expensive to do variable-base MSMs in a circuit \(\implies\) non-native field arithmetic
ECCVM
- Aim: To efficiently evaluate variable-base EC operations over a SNARK-friendly embedded curve
- To be integrated as a component of Goblin Plonk
- The EC operations would be evaluated over the curve \(\mathbb{G}\in\mathbb{F}_q^2, \ r := |\mathbb{G}|\)
\begin{aligned}
P_{\textsf{right}} =&\ \textcolor{olive}{\mathfrak{z}}\cdot \textcolor{orange}{[W_1]} +
\textcolor{olive}{u\mathfrak{z}\omega}\cdot \textcolor{orange}{[W_2]} +
\textcolor{olive}{s}\cdot \textcolor{brown}{[1]}
\ + \\[3pt]
&\ \textcolor{olive}{v}\cdot \textcolor{orange}{[a]} +
\textcolor{olive}{v^2}\cdot \textcolor{orange}{[b]} +
\textcolor{olive}{v^3}\cdot \textcolor{orange}{[c]} +
\textcolor{olive}{v^4}\cdot \textcolor{brown}{[s_{\sigma_1}]} +
\textcolor{olive}{v^5}\cdot \textcolor{brown}{[s_{\sigma_2}]}
\ + \\[3pt]
&\ \textcolor{olive}{\bar{a}\bar{b}}\cdot \textcolor{brown}{[q_m]} +
\textcolor{olive}{\bar{a}}\cdot \textcolor{brown}{[q_l]} +
\textcolor{olive}{\bar{b}}\cdot \textcolor{brown}{[q_r]} +
\textcolor{olive}{\bar{c}}\cdot \textcolor{brown}{[q_o]} +
\textcolor{olive}{1}\cdot \textcolor{brown}{[q_c]}
\ + \\[3pt]
&\ \textcolor{olive}{s_2}\cdot \textcolor{orange}{[z]} +
\textcolor{olive}{s_3}\cdot \textcolor{brown}{[s_{\sigma_3}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}}\cdot \textcolor{orange}{[t_{lo}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^n}\cdot \textcolor{orange}{[t_{mid}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^{2n}}\cdot \textcolor{orange}{[t_{hi}]}
\end{aligned}
\textsf{eq}
\textsf{add}
\textsf{mul}
Opcodes
\textsf{add}(\textcolor{orange}{P}) : \ \ A \leftarrow A + \textcolor{orange}{P}
- We need an accumulator \(A\) to record the result of the EC operations
- The set of opcodes we want to support is:
\textsf{mul}(\textcolor{orange}{P}, \textcolor{olive}{s}): \ \ A \leftarrow A + \textcolor{olive}{s} \cdot \textcolor{orange}{P}
\textsf{eq}(\textcolor{orange}{P}) : \ \ A \stackrel{?}{=} \textcolor{orange}{P}
\textsf{reset} : \ \ A \leftarrow \mathcal{O}
- For the multiplication op, we need to split scalar \(\textcolor{olive}{s}\in\mathbb{F}_r\) as:
\textcolor{olive}{s} = \textcolor{olive}{z_1} + \lambda\textcolor{olive}{z_2}
- Here \(\textcolor{olive}{z_1}, \textcolor{olive}{z_2}\) are 128-bit scalars, \(\lambda \in \mathbb{F}_r\) is the cube-root of unity
\implies \textcolor{olive}{s}\cdot P = \textcolor{olive}{z_1}\cdot P + \textcolor{olive}{z_2}\cdot P'
Roadmap
- We will split the ECCVM discussion in three parts:
- ECCVM Transcript
- ECCVM pre-computation
- ECCVM MSM computation
- We will cover the following preliminaries:
- \(w\)NAF for scalars
- Strauss MSM algorithm and the
- Our takeaway should be the design process of the ECCVM
\(w\)NAF Form
- \(w\)NAF stands for windowed non-adjacent form
- It is a signed-digit representation, in which non-zero values are non-adjacent
- We can represent integer \(11\) in the following forms:
\begin{matrix}
(0 & 1 & 0 & 1 & 1) & \equiv & (8+2+1) & =11 \\[2pt]
(0 & 1 & 1 & 0 & -1) & \equiv & (8+4-1) & =11 \\[2pt]
(\textcolor{red}{1} & \color{red}{0} & \color{red}{-1} & \color{red}{0} & \textcolor{red}{-1}) & \equiv & (16-4-1) & =11 \\[2pt]
(1 & -1 & 1 & 0 & -1) & \equiv & (16-8+4-1) & =11 \\[2pt]
(1 & -1 & 0 & 1 & 1) & \equiv & (16-8+2+1) & =11
\end{matrix}
- Only the third example is a non-adjacent form in digits \(\{-1,0,1\}\)
- The bit-size of the slices is known as the window size (here, \(w = 2\))
- Used primarily for efficient scalar multiplication computation
- To compute \(11\cdot G,\) we only need 3 (2-bit) scalar multiplications
\(w\)NAF Form
- Minimal example: 8-bit scalar \(b=25\) and window \(w=2\)
b = 25 \equiv (\textcolor{olive}{00 \quad 01 \quad 10 \quad 01})
\begin{aligned}
\implies b\cdot\textcolor{orange}{P} = \sum_{i=0}^{\frac{|b|}{w}} \textcolor{olive}{w_i} \cdot \textcolor{orange}{2^{w \cdot i} P}
\end{aligned}
- We want to avoid zeros in \(w\)NAF to avoid conditional EC additions
- Lets map the slices values to \(\{-3, -1, 1, 3\}\) instead of \(\{0,1,2,3\}\)
b = 25 \equiv (\textcolor{olive}{00 \quad 01 \quad 10 \quad 01})
\equiv \textcolor{olive}{1}\cdot \textcolor{orange}{2^{2\cdot 3}}
+
\textcolor{olive}{(-3)}\cdot \textcolor{orange}{2^{2\cdot 2}}
+
\textcolor{olive}{3}\cdot \textcolor{orange}{2^{2\cdot 1}}
+
\textcolor{olive}{(-3)}\cdot \textcolor{orange}{2^{2\cdot 0}}
= 64 - 48 + 12 - 3
= 25
- But how do we represent even numbers? Add a skew bit!
\implies b = \sum_{i=0}^{\frac{|b|}{w}} \textcolor{olive}{w_i} \cdot \textcolor{orange}{2^{w \cdot i}} - \textsf{skew}
0
1
2
1
1
-3
3
-3
\{0: \textcolor{grey}{\textsf{odd}},\ 1: \textcolor{grey}{\textsf{even}}\}
More on \(w\)NAF

Strauss MSM
- The main aim is to compute an MSM of the form:
\begin{aligned}
A = \sum_{i=1}^{m}
\textcolor{olive}{s_i} \cdot
\textcolor{orange}{[P_i]}
\end{aligned}
- Scalars \(\{\textcolor{olive}{s_i}\}\) are assumed to be 128-bit numbers
- We split the scalars into their \(w\)NAF form s.t. \(w=4\): (read \(w\)NAF notes here)
\begin{aligned}
\implies A = \sum_{i=1}^{m}
\left(
\textcolor{grey}{\overbrace{\textcolor{olive}{\underbrace{1010}_{w_{i,31}} \ \underbrace{0010}_{w_{i,30}} \ \dots \ \underbrace{1110}_{w_{i,2}} \ \underbrace{1001}_{w_{i,1}} \ \underbrace{1011}_{w_{i,0}}}}^{32 \times 4 = 128 \text{ bits}}}
\right)
\cdot \textcolor{orange}{[P_i]}
\end{aligned}
\begin{aligned}
\implies A = \sum_{i=1}^{m}
\left(
\textcolor{olive}{\sum_{j=0}^{31} 2^{4j}\cdot w_{i,j} - \textsf{skew}_i}
\right)
\cdot \textcolor{orange}{[P_i]}
\end{aligned}
\begin{aligned}
\implies A = \sum_{i=1}^{m}
\left(
\sum_{j=0}^{31} \textcolor{olive}{w_{i,j}}\cdot\textcolor{orange}{[2^{4j} \cdot P_i]}
- \textcolor{olive}{\textsf{skew}_i}\cdot\textcolor{orange}{[P_i]}
\right)
\end{aligned}
\overbrace{\hspace{3cm}}
Precomputation
\underbrace{\hspace{8cm}}
Actual MSM
ECCVM Transcript
\begin{aligned}
\textcolor{grey}{P_{\textsf{right}}} =&\ \textcolor{olive}{\mathfrak{z}}\cdot \textcolor{orange}{[W_1]} +
\textcolor{olive}{u\mathfrak{z}\omega}\cdot \textcolor{orange}{[W_2]} +
\textcolor{olive}{s}\cdot \textcolor{brown}{[1]}
\ + \\[3pt]
&\ \textcolor{olive}{v}\cdot \textcolor{orange}{[a]} +
\textcolor{olive}{v^2}\cdot \textcolor{orange}{[b]} +
\textcolor{olive}{v^3}\cdot \textcolor{orange}{[c]} +
\textcolor{olive}{v^4}\cdot \textcolor{brown}{[s_{\sigma_1}]} +
\textcolor{olive}{v^5}\cdot \textcolor{brown}{[s_{\sigma_2}]}
\ + \\[3pt]
&\ \textcolor{olive}{\bar{a}\bar{b}}\cdot \textcolor{brown}{[q_m]} +
\textcolor{olive}{\bar{a}}\cdot \textcolor{brown}{[q_l]} +
\textcolor{olive}{\bar{b}}\cdot \textcolor{brown}{[q_r]} +
\textcolor{olive}{\bar{c}}\cdot \textcolor{brown}{[q_o]} +
\textcolor{olive}{1}\cdot \textcolor{brown}{[q_c]}
\ + \\[3pt]
&\ \textcolor{olive}{s_2}\cdot \textcolor{orange}{[z]} +
\textcolor{olive}{s_3}\cdot \textcolor{brown}{[s_{\sigma_3}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}}\cdot \textcolor{orange}{[t_{lo}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^n}\cdot \textcolor{orange}{[t_{mid}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^{2n}}\cdot \textcolor{orange}{[t_{hi}]}
\end{aligned}
\textcolor{grey}{P_{\textsf{left}}} = \textcolor{olive}{1}\cdot \textcolor{orange}{[W_1]} + \textcolor{olive}{u}\cdot \textcolor{orange}{[W_2]}
\textsf{mul}
[W_1]_x
[W_1]_y
1
0
25
0
0
1
[W_1]_x
[W_1]_y
\text{true}
| Op | PC | MC | |||||||
P_x
P_y
z_1
z_2
A_x
A_y
M_x
M_y
A = \mathcal{O}
ECCVM Transcript
\begin{aligned}
\textcolor{grey}{P_{\textsf{right}}} =&\ \textcolor{olive}{\mathfrak{z}}\cdot \textcolor{orange}{[W_1]} +
\textcolor{olive}{u\mathfrak{z}\omega}\cdot \textcolor{orange}{[W_2]} +
\textcolor{olive}{s}\cdot \textcolor{brown}{[1]}
\ + \\[3pt]
&\ \textcolor{olive}{v}\cdot \textcolor{orange}{[a]} +
\textcolor{olive}{v^2}\cdot \textcolor{orange}{[b]} +
\textcolor{olive}{v^3}\cdot \textcolor{orange}{[c]} +
\textcolor{olive}{v^4}\cdot \textcolor{brown}{[s_{\sigma_1}]} +
\textcolor{olive}{v^5}\cdot \textcolor{brown}{[s_{\sigma_2}]}
\ + \\[3pt]
&\ \textcolor{olive}{\bar{a}\bar{b}}\cdot \textcolor{brown}{[q_m]} +
\textcolor{olive}{\bar{a}}\cdot \textcolor{brown}{[q_l]} +
\textcolor{olive}{\bar{b}}\cdot \textcolor{brown}{[q_r]} +
\textcolor{olive}{\bar{c}}\cdot \textcolor{brown}{[q_o]} +
\textcolor{olive}{1}\cdot \textcolor{brown}{[q_c]}
\ + \\[3pt]
&\ \textcolor{olive}{s_2}\cdot \textcolor{orange}{[z]} +
\textcolor{olive}{s_3}\cdot \textcolor{brown}{[s_{\sigma_3}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}}\cdot \textcolor{orange}{[t_{lo}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^n}\cdot \textcolor{orange}{[t_{mid}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^{2n}}\cdot \textcolor{orange}{[t_{hi}]}
\end{aligned}
| Op | PC | MC | |||||||
\textcolor{grey}{P_{\textsf{left}}} = \textcolor{olive}{1}\cdot \textcolor{orange}{[W_1]} + \textcolor{olive}{u}\cdot \textcolor{orange}{[W_2]}
P_x
P_y
z_1
z_2
A_x
A_y
M_x
M_y
A = \mathcal{O}
\textsf{mul}
[W_1]_x
[W_1]_y
1
0
25
0
0
1
[W_1]_x
[W_1]_y
\text{true}
\textsf{mul}
[W_2]_x
[W_2]_y
u
0
24
2
[P_{\textsf{left}}]_x
[P_{\textsf{left}}]_y
\text{false}
[P_{\textsf{left}}]_x
[P_{\textsf{left}}]_y
ECCVM Transcript
\begin{aligned}
\textcolor{grey}{P_{\textsf{right}}} =&\ \textcolor{olive}{\mathfrak{z}}\cdot \textcolor{orange}{[W_1]} +
\textcolor{olive}{u\mathfrak{z}\omega}\cdot \textcolor{orange}{[W_2]} +
\textcolor{olive}{s}\cdot \textcolor{brown}{[1]}
\ + \\[3pt]
&\ \textcolor{olive}{v}\cdot \textcolor{orange}{[a]} +
\textcolor{olive}{v^2}\cdot \textcolor{orange}{[b]} +
\textcolor{olive}{v^3}\cdot \textcolor{orange}{[c]} +
\textcolor{olive}{v^4}\cdot \textcolor{brown}{[s_{\sigma_1}]} +
\textcolor{olive}{v^5}\cdot \textcolor{brown}{[s_{\sigma_2}]}
\ + \\[3pt]
&\ \textcolor{olive}{\bar{a}\bar{b}}\cdot \textcolor{brown}{[q_m]} +
\textcolor{olive}{\bar{a}}\cdot \textcolor{brown}{[q_l]} +
\textcolor{olive}{\bar{b}}\cdot \textcolor{brown}{[q_r]} +
\textcolor{olive}{\bar{c}}\cdot \textcolor{brown}{[q_o]} +
\textcolor{olive}{1}\cdot \textcolor{brown}{[q_c]}
\ + \\[3pt]
&\ \textcolor{olive}{s_2}\cdot \textcolor{orange}{[z]} +
\textcolor{olive}{s_3}\cdot \textcolor{brown}{[s_{\sigma_3}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}}\cdot \textcolor{orange}{[t_{lo}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^n}\cdot \textcolor{orange}{[t_{mid}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^{2n}}\cdot \textcolor{orange}{[t_{hi}]}
\end{aligned}
| Op | PC | MC | |||||||
\textcolor{grey}{P_{\textsf{left}}} = \textcolor{olive}{1}\cdot \textcolor{orange}{[W_1]} + \textcolor{olive}{u}\cdot \textcolor{orange}{[W_2]}
P_x
P_y
z_1
z_2
A_x
A_y
M_x
M_y
A = \mathcal{O}
\textsf{mul}
[W_1]_x
[W_1]_y
1
0
25
0
0
1
[W_1]_x
[W_1]_y
\text{true}
\textsf{mul}
[W_2]_x
[W_2]_y
u
0
24
2
[P_{\textsf{left}}]_x
[P_{\textsf{left}}]_y
\text{false}
[P_{\textsf{left}}]_x
[P_{\textsf{left}}]_y
\textsf{mul}
[W_1]_x
[W_1]_y
\mathfrak{z}
0
23
1
\textcolor{olive}{\mathfrak{z}}\textcolor{orange}{[W_1]_x}
\text{true}
\textcolor{olive}{\mathfrak{z}}\textcolor{orange}{[W_1]_y}
0
0
ECCVM Transcript
\begin{aligned}
\textcolor{grey}{P_{\textsf{right}}} =&\ \textcolor{olive}{\mathfrak{z}}\cdot \textcolor{orange}{[W_1]} +
\textcolor{olive}{u\mathfrak{z}\omega}\cdot \textcolor{orange}{[W_2]} +
\textcolor{olive}{s}\cdot \textcolor{brown}{[1]}
\ + \\[3pt]
&\ \textcolor{olive}{v}\cdot \textcolor{orange}{[a]} +
\textcolor{olive}{v^2}\cdot \textcolor{orange}{[b]} +
\textcolor{olive}{v^3}\cdot \textcolor{orange}{[c]} +
\textcolor{olive}{v^4}\cdot \textcolor{brown}{[s_{\sigma_1}]} +
\textcolor{olive}{v^5}\cdot \textcolor{brown}{[s_{\sigma_2}]}
\ + \\[3pt]
&\ \textcolor{olive}{\bar{a}\bar{b}}\cdot \textcolor{brown}{[q_m]} +
\textcolor{olive}{\bar{a}}\cdot \textcolor{brown}{[q_l]} +
\textcolor{olive}{\bar{b}}\cdot \textcolor{brown}{[q_r]} +
\textcolor{olive}{\bar{c}}\cdot \textcolor{brown}{[q_o]} +
\textcolor{olive}{1}\cdot \textcolor{brown}{[q_c]}
\ + \\[3pt]
&\ \textcolor{olive}{s_2}\cdot \textcolor{orange}{[z]} +
\textcolor{olive}{s_3}\cdot \textcolor{brown}{[s_{\sigma_3}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}}\cdot \textcolor{orange}{[t_{lo}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^n}\cdot \textcolor{orange}{[t_{mid}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^{2n}}\cdot \textcolor{orange}{[t_{hi}]}
\end{aligned}
| Op | PC | MC | |||||||
\textcolor{grey}{P_{\textsf{left}}} = \textcolor{olive}{1}\cdot \textcolor{orange}{[W_1]} + \textcolor{olive}{u}\cdot \textcolor{orange}{[W_2]}
P_x
P_y
z_1
z_2
A_x
A_y
M_x
M_y
A = \mathcal{O}
\textsf{mul}
[W_1]_x
[W_1]_y
1
0
25
0
0
1
[W_1]_x
[W_1]_y
\text{true}
\textsf{mul}
[W_2]_x
[W_2]_y
u
0
24
2
[P_{\textsf{left}}]_x
[P_{\textsf{left}}]_y
\text{false}
\textsf{mul}
[W_1]_x
[W_1]_y
\mathfrak{z}
0
23
1
\textcolor{olive}{\mathfrak{z}}\textcolor{orange}{[W_1]_x}
[P_{\textsf{left}}]_x
[P_{\textsf{left}}]_y
\text{true}
\textcolor{olive}{\mathfrak{z}}\textcolor{orange}{[W_1]_y}
0
0
\textsf{mul}
[W_2]_x
[W_2]_y
(u\mathfrak{z}\omega)_1
21
3
+\textcolor{olive}{u\mathfrak{z}\omega}[W_2]_x
\text{true}
(u\mathfrak{z}\omega)_2
+\textcolor{olive}{u\mathfrak{z}\omega}[W_2]_y
0
0
ECCVM Transcript
\begin{aligned}
\textcolor{grey}{P_{\textsf{right}}} =&\ \textcolor{olive}{\mathfrak{z}}\cdot \textcolor{orange}{[W_1]} +
\textcolor{olive}{u\mathfrak{z}\omega}\cdot \textcolor{orange}{[W_2]} +
\textcolor{olive}{s}\cdot \textcolor{brown}{[1]}
\ + \\[3pt]
&\ \textcolor{olive}{v}\cdot \textcolor{orange}{[a]} +
\textcolor{olive}{v^2}\cdot \textcolor{orange}{[b]} +
\textcolor{olive}{v^3}\cdot \textcolor{orange}{[c]} +
\textcolor{olive}{v^4}\cdot \textcolor{brown}{[s_{\sigma_1}]} +
\textcolor{olive}{v^5}\cdot \textcolor{brown}{[s_{\sigma_2}]}
\ + \\[3pt]
&\ \textcolor{olive}{\bar{a}\bar{b}}\cdot \textcolor{brown}{[q_m]} +
\textcolor{olive}{\bar{a}}\cdot \textcolor{brown}{[q_l]} +
\textcolor{olive}{\bar{b}}\cdot \textcolor{brown}{[q_r]} +
\textcolor{olive}{\bar{c}}\cdot \textcolor{brown}{[q_o]} +
\textcolor{olive}{1}\cdot \textcolor{brown}{[q_c]}
\ + \\[3pt]
&\ \textcolor{olive}{s_2}\cdot \textcolor{orange}{[z]} +
\textcolor{olive}{s_3}\cdot \textcolor{brown}{[s_{\sigma_3}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}}\cdot \textcolor{orange}{[t_{lo}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^n}\cdot \textcolor{orange}{[t_{mid}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^{2n}}\cdot \textcolor{orange}{[t_{hi}]}
\end{aligned}
| Op | PC | MC | |||||||
\textcolor{grey}{P_{\textsf{left}}} = \textcolor{olive}{1}\cdot \textcolor{orange}{[W_1]} + \textcolor{olive}{u}\cdot \textcolor{orange}{[W_2]}
P_x
P_y
z_1
z_2
A_x
A_y
M_x
M_y
A = \mathcal{O}
\textsf{mul}
[W_1]_x
[W_1]_y
1
0
25
0
0
1
[W_1]_x
[W_1]_y
\text{true}
\textsf{mul}
[W_2]_x
[W_2]_y
u
0
24
2
[P_{\textsf{left}}]_x
[P_{\textsf{left}}]_y
\text{false}
\textsf{mul}
[W_1]_x
[W_1]_y
\mathfrak{z}
0
23
1
\textcolor{olive}{\mathfrak{z}}\textcolor{orange}{[W_1]_x}
[P_{\textsf{left}}]_x
[P_{\textsf{left}}]_y
\text{true}
\textsf{mul}
[W_2]_x
[W_2]_y
(u\mathfrak{z}\omega)_1
21
3
+\textcolor{olive}{u\mathfrak{z}\omega}[W_2]_x
\text{true}
(u\mathfrak{z}\omega)_2
\textcolor{olive}{\mathfrak{z}}\textcolor{orange}{[W_1]_y}
+\textcolor{olive}{u\mathfrak{z}\omega}[W_2]_y
0
0
0
0
\textsf{mul}
[1]_x
[1]_y
s
20
4
+\textcolor{olive}{s}[1]_x
\text{true}
0
+\textcolor{olive}{s}[1]_y
0
0
ECCVM Transcript
\begin{aligned}
\textcolor{grey}{P_{\textsf{right}}} =&\ \textcolor{olive}{\mathfrak{z}}\cdot \textcolor{orange}{[W_1]} +
\textcolor{olive}{u\mathfrak{z}\omega}\cdot \textcolor{orange}{[W_2]} +
\textcolor{olive}{s}\cdot \textcolor{brown}{[1]}
\ + \\[3pt]
&\ \textcolor{olive}{v}\cdot \textcolor{orange}{[a]} +
\textcolor{olive}{v^2}\cdot \textcolor{orange}{[b]} +
\textcolor{olive}{v^3}\cdot \textcolor{orange}{[c]} +
\textcolor{olive}{v^4}\cdot \textcolor{brown}{[s_{\sigma_1}]} +
\textcolor{olive}{v^5}\cdot \textcolor{brown}{[s_{\sigma_2}]}
\ + \\[3pt]
&\ \textcolor{olive}{\bar{a}\bar{b}}\cdot \textcolor{brown}{[q_m]} +
\textcolor{olive}{\bar{a}}\cdot \textcolor{brown}{[q_l]} +
\textcolor{olive}{\bar{b}}\cdot \textcolor{brown}{[q_r]} +
\textcolor{olive}{\bar{c}}\cdot \textcolor{brown}{[q_o]} +
\textcolor{olive}{1}\cdot \textcolor{brown}{[q_c]}
\ + \\[3pt]
&\ \textcolor{olive}{s_2}\cdot \textcolor{orange}{[z]} +
\textcolor{olive}{s_3}\cdot \textcolor{brown}{[s_{\sigma_3}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}}\cdot \textcolor{orange}{[t_{lo}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^n}\cdot \textcolor{orange}{[t_{mid}]} +
\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^{2n}}\cdot \textcolor{orange}{[t_{hi}]}
\end{aligned}
| Op | PC | MC | |||||||
\textcolor{grey}{P_{\textsf{left}}} = \textcolor{olive}{1}\cdot \textcolor{orange}{[W_1]} + \textcolor{olive}{u}\cdot \textcolor{orange}{[W_2]}
P_x
P_y
z_1
z_2
A_x
A_y
M_x
M_y
A = \mathcal{O}
\textsf{mul}
[W_1]_x
[W_1]_y
1
0
25
0
0
1
[W_1]_x
[W_1]_y
\text{true}
\textsf{mul}
[W_2]_x
[W_2]_y
u
0
24
2
[P_{\textsf{left}}]_x
[P_{\textsf{left}}]_y
\text{false}
\textsf{mul}
[W_1]_x
[W_1]_y
\mathfrak{z}
0
23
1
\textcolor{olive}{\mathfrak{z}}\textcolor{orange}{[W_1]_x}
[P_{\textsf{left}}]_x
[P_{\textsf{left}}]_y
\text{true}
\textsf{mul}
[W_2]_x
[W_2]_y
(u\mathfrak{z}\omega)_1
21
3
+\textcolor{olive}{u\mathfrak{z}\omega}[W_2]_x
\text{true}
(u\mathfrak{z}\omega)_2
\textsf{mul}
[1]_x
[1]_y
s
20
4
+\textcolor{olive}{s}[1]_x
\text{true}
0
\textcolor{olive}{\mathfrak{z}}\textcolor{orange}{[W_1]_y}
+\textcolor{olive}{u\mathfrak{z}\omega}[W_2]_y
+\textcolor{olive}{s}[1]_y
0
0
0
0
0
0
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\textsf{mul}
[t_{hi}]_x
[t_{hi}]_y
(\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^{2n}})_1
1
23
+\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^{2n}}\cdot \textcolor{orange}{[t_{hi}]}_x
\text{false}
[P_{\textsf{right}}]_x
[P_{\textsf{right}}]_y
+\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^{2n}}\cdot \textcolor{orange}{[t_{hi}]}_y
(\textcolor{olive}{\bar{z}_{\mathbb{H}}\mathfrak{z}^{2n}})_2
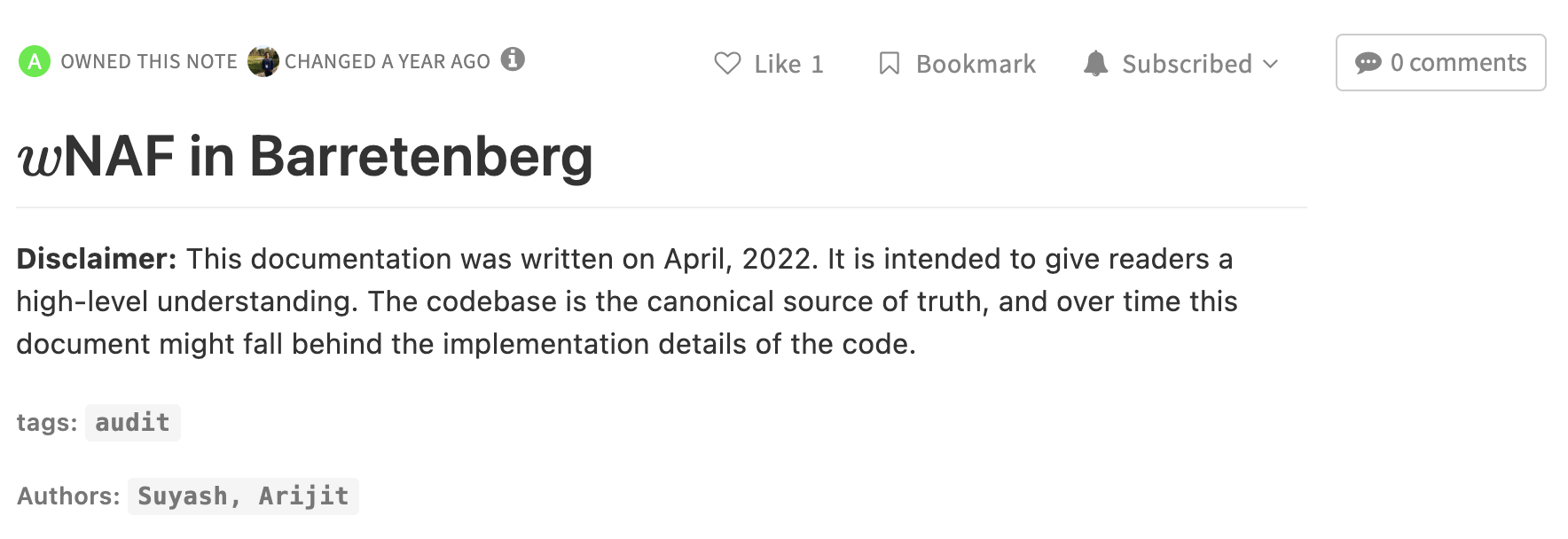
Precomputation in ECCVM
\begin{aligned}
\implies A = \sum_{i=1}^{m}
\left(
\sum_{j=0}^{31} \textcolor{olive}{w_{i,j}}\cdot\textcolor{orange}{[2^{4j} \cdot P_i]}
- \textcolor{olive}{\textsf{skew}_i}\cdot\textcolor{orange}{[P_i]}
\right)
\end{aligned}
\overbrace{\hspace{3cm}}
Precomputation
| Pre | PC | Tran | Round | ||||||
| 1 | 2 | 0 | 0 | 0 | |||||
| 1 | 2 | 0 | 1 | 0 | |||||
| 1 | 2 | 0 | 2 | 0 | |||||
| 1 | 2 | 0 | 3 | 0 | |||||
| 1 | 2 | 0 | 4 | 0 | |||||
| 1 | 2 | 0 | 5 | 0 | |||||
| 1 | 2 | 0 | 6 | 0 | |||||
| 1 | 2 | 7 | |||||||
| 1 | 0 | 0 |
\sum_j w_{i,j}
\textsf{skew}_i
[T_i]
w_{i,\textsf{row}}
w_{i,\textsf{row} + 1}
w_{i,\textsf{row} + 2}
w_{i,\textsf{row} + 3}
[D_i]
1
1
w_{i,0}
w_{i,1}
w_{i,2}
w_{i,3}
w_{i,4}
w_{i,5}
w_{i,6}
w_{i,7}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
w_{i,28}
w_{i,29}
w_{i,30}
w_{i,31}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\sum_4 w_{i,j}
\sum_8 w_{i,j}
\sum_{12} w_{i,j}
s_i = \sum_{32} w_{i,j}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\{0,1\}
[15\cdot P_i]
[13\cdot P_i]
[11\cdot P_i]
[9\cdot P_i]
[7\cdot P_i]
[5\cdot P_i]
[3\cdot P_i]
[P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
Precomputation in ECCVM
\begin{aligned}
\implies A = \sum_{i=1}^{m}
\left(
\sum_{j=0}^{31} \textcolor{olive}{w_{i,j}}\cdot\textcolor{orange}{[2^{4j} \cdot P_i]}
- \textcolor{olive}{\textsf{skew}_i}\cdot\textcolor{orange}{[P_i]}
\right)
\end{aligned}
\overbrace{\hspace{3cm}}
Precomputation
| Pre | PC | Tran | Round | ||||||
| 1 | 2 | 0 | 0 | 0 | |||||
| 1 | 2 | 0 | 1 | 0 | |||||
| 1 | 2 | 0 | 2 | 0 | |||||
| 1 | 2 | 0 | 3 | 0 | |||||
| 1 | 2 | 0 | 4 | 0 | |||||
| 1 | 2 | 0 | 5 | 0 | |||||
| 1 | 2 | 0 | 6 | 0 | |||||
| 1 | 2 | 7 | |||||||
| 1 | 0 | 0 |
\sum_j w_{i,j}
\textsf{skew}_i
[T_i]
w_{i,\textsf{row}}
w_{i,\textsf{row} + 1}
w_{i,\textsf{row} + 2}
w_{i,\textsf{row} + 3}
[D_i]
1
1
w_{i,0}
w_{i,1}
w_{i,2}
w_{i,3}
w_{i,4}
w_{i,5}
w_{i,6}
w_{i,7}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
w_{i,28}
w_{i,29}
w_{i,30}
w_{i,31}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\sum_4 w_{i,j}
\sum_8 w_{i,j}
\sum_{12} w_{i,j}
s_i = \sum_{32} w_{i,j}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\{0,1\}
[15\cdot P_i]
[13\cdot P_i]
[11\cdot P_i]
[9\cdot P_i]
[7\cdot P_i]
[5\cdot P_i]
[3\cdot P_i]
[P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
Precomputation in ECCVM
\begin{aligned}
\implies A = \sum_{i=1}^{m}
\left(
\sum_{j=0}^{31} \textcolor{olive}{w_{i,j}}\cdot\textcolor{orange}{[2^{4j} \cdot P_i]}
- \textcolor{olive}{\textsf{skew}_i}\cdot\textcolor{orange}{[P_i]}
\right)
\end{aligned}
\overbrace{\hspace{3cm}}
Precomputation
| Pre | PC | Tran | Round | ||||||
| 1 | 2 | 0 | 0 | 0 | |||||
| 1 | 2 | 0 | 1 | 0 | |||||
| 1 | 2 | 0 | 2 | 0 | |||||
| 1 | 2 | 0 | 3 | 0 | |||||
| 1 | 2 | 0 | 4 | 0 | |||||
| 1 | 2 | 0 | 5 | 0 | |||||
| 1 | 2 | 0 | 6 | 0 | |||||
| 1 | 2 | 7 | |||||||
| 1 | 0 | 0 |
\sum_j w_{i,j}
\textsf{skew}_i
[T_i]
w_{i,\textsf{row}}
w_{i,\textsf{row} + 1}
w_{i,\textsf{row} + 2}
w_{i,\textsf{row} + 3}
[D_i]
1
1
w_{i,0}
w_{i,1}
w_{i,2}
w_{i,3}
w_{i,4}
w_{i,5}
w_{i,6}
w_{i,7}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
w_{i,28}
w_{i,29}
w_{i,30}
w_{i,31}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\sum_4 w_{i,j}
\sum_8 w_{i,j}
\sum_{12} w_{i,j}
s_i = \sum_{32} w_{i,j}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\{0,1\}
[15\cdot P_i]
[13\cdot P_i]
[11\cdot P_i]
[9\cdot P_i]
[7\cdot P_i]
[5\cdot P_i]
[3\cdot P_i]
[P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
Precomputation in ECCVM
\begin{aligned}
\implies A = \sum_{i=1}^{m}
\left(
\sum_{j=0}^{31} \textcolor{olive}{w_{i,j}}\cdot\textcolor{orange}{[2^{4j} \cdot P_i]}
- \textcolor{olive}{\textsf{skew}_i}\cdot\textcolor{orange}{[P_i]}
\right)
\end{aligned}
\overbrace{\hspace{3cm}}
Precomputation
| Pre | PC | Tran | Round | ||||||
| 1 | 2 | 0 | 0 | 0 | |||||
| 1 | 2 | 0 | 1 | 0 | |||||
| 1 | 2 | 0 | 2 | 0 | |||||
| 1 | 2 | 0 | 3 | 0 | |||||
| 1 | 2 | 0 | 4 | 0 | |||||
| 1 | 2 | 0 | 5 | 0 | |||||
| 1 | 2 | 0 | 6 | 0 | |||||
| 1 | 2 | 7 | |||||||
| 1 | 0 | 0 |
\sum_j w_{i,j}
\textsf{skew}_i
[T_i]
w_{i,\textsf{row}}
w_{i,\textsf{row} + 1}
w_{i,\textsf{row} + 2}
w_{i,\textsf{row} + 3}
[D_i]
1
1
w_{i,0}
w_{i,1}
w_{i,2}
w_{i,3}
w_{i,4}
w_{i,5}
w_{i,6}
w_{i,7}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
w_{i,28}
w_{i,29}
w_{i,30}
w_{i,31}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\sum_4 w_{i,j}
\sum_8 w_{i,j}
\sum_{12} w_{i,j}
s_i = \sum_{32} w_{i,j}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\{0,1\}
[15\cdot P_i]
[13\cdot P_i]
[11\cdot P_i]
[9\cdot P_i]
[7\cdot P_i]
[5\cdot P_i]
[3\cdot P_i]
[P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
Precomputation in ECCVM
\begin{aligned}
\implies A = \sum_{i=1}^{m}
\left(
\sum_{j=0}^{31} \textcolor{olive}{w_{i,j}}\cdot\textcolor{orange}{[2^{4j} \cdot P_i]}
- \textcolor{olive}{\textsf{skew}_i}\cdot\textcolor{orange}{[P_i]}
\right)
\end{aligned}
\overbrace{\hspace{3cm}}
Precomputation
| Pre | PC | Tran | Round | ||||||
| 1 | 2 | 0 | 0 | 0 | |||||
| 1 | 2 | 0 | 1 | 0 | |||||
| 1 | 2 | 0 | 2 | 0 | |||||
| 1 | 2 | 0 | 3 | 0 | |||||
| 1 | 2 | 0 | 4 | 0 | |||||
| 1 | 2 | 0 | 5 | 0 | |||||
| 1 | 2 | 0 | 6 | 0 | |||||
| 1 | 2 | 7 | |||||||
| 1 | 0 | 0 |
\sum_j w_{i,j}
\textsf{skew}_i
[T_i]
w_{i,\textsf{row}}
w_{i,\textsf{row} + 1}
w_{i,\textsf{row} + 2}
w_{i,\textsf{row} + 3}
[D_i]
1
1
w_{i,0}
w_{i,1}
w_{i,2}
w_{i,3}
w_{i,4}
w_{i,5}
w_{i,6}
w_{i,7}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
w_{i,28}
w_{i,29}
w_{i,30}
w_{i,31}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\sum_4 w_{i,j}
\sum_8 w_{i,j}
\sum_{12} w_{i,j}
s_i = \sum_{32} w_{i,j}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\{0,1\}
[15\cdot P_i]
[13\cdot P_i]
[11\cdot P_i]
[9\cdot P_i]
[7\cdot P_i]
[5\cdot P_i]
[3\cdot P_i]
[P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
1 scalar = 8 rows
Precomputation in ECCVM
\begin{aligned}
\implies A = \sum_{i=1}^{m}
\left(
\sum_{j=0}^{31} \textcolor{olive}{w_{i,j}}\cdot\textcolor{orange}{[2^{4j} \cdot P_i]}
- \textcolor{olive}{\textsf{skew}_i}\cdot\textcolor{orange}{[P_i]}
\right)
\end{aligned}
\overbrace{\hspace{3cm}}
Precomputation
| Pre | PC | Tran | Round | ||||||
| 1 | 2 | 0 | 0 | 0 | |||||
| 1 | 2 | 0 | 1 | 0 | |||||
| 1 | 2 | 0 | 2 | 0 | |||||
| 1 | 2 | 0 | 3 | 0 | |||||
| 1 | 2 | 0 | 4 | 0 | |||||
| 1 | 2 | 0 | 5 | 0 | |||||
| 1 | 2 | 0 | 6 | 0 | |||||
| 1 | 2 | 7 | |||||||
| 1 | 0 | 0 |
\sum_j w_{i,j}
\textsf{skew}_i
[T_i]
w_{i,\textsf{row}}
w_{i,\textsf{row} + 1}
w_{i,\textsf{row} + 2}
w_{i,\textsf{row} + 3}
[D_i]
1
1
w_{i,0}
w_{i,1}
w_{i,2}
w_{i,3}
w_{i,4}
w_{i,5}
w_{i,6}
w_{i,7}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
w_{i,28}
w_{i,29}
w_{i,30}
w_{i,31}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\sum_4 w_{i,j}
\sum_8 w_{i,j}
\sum_{12} w_{i,j}
s_i = \sum_{32} w_{i,j}
\vdots\\[10pt]
\vdots\\[10pt]
\vdots
\{0,1\}
[15\cdot P_i]
[13\cdot P_i]
[11\cdot P_i]
[9\cdot P_i]
[7\cdot P_i]
[5\cdot P_i]
[3\cdot P_i]
[P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
[2\cdot P_i]
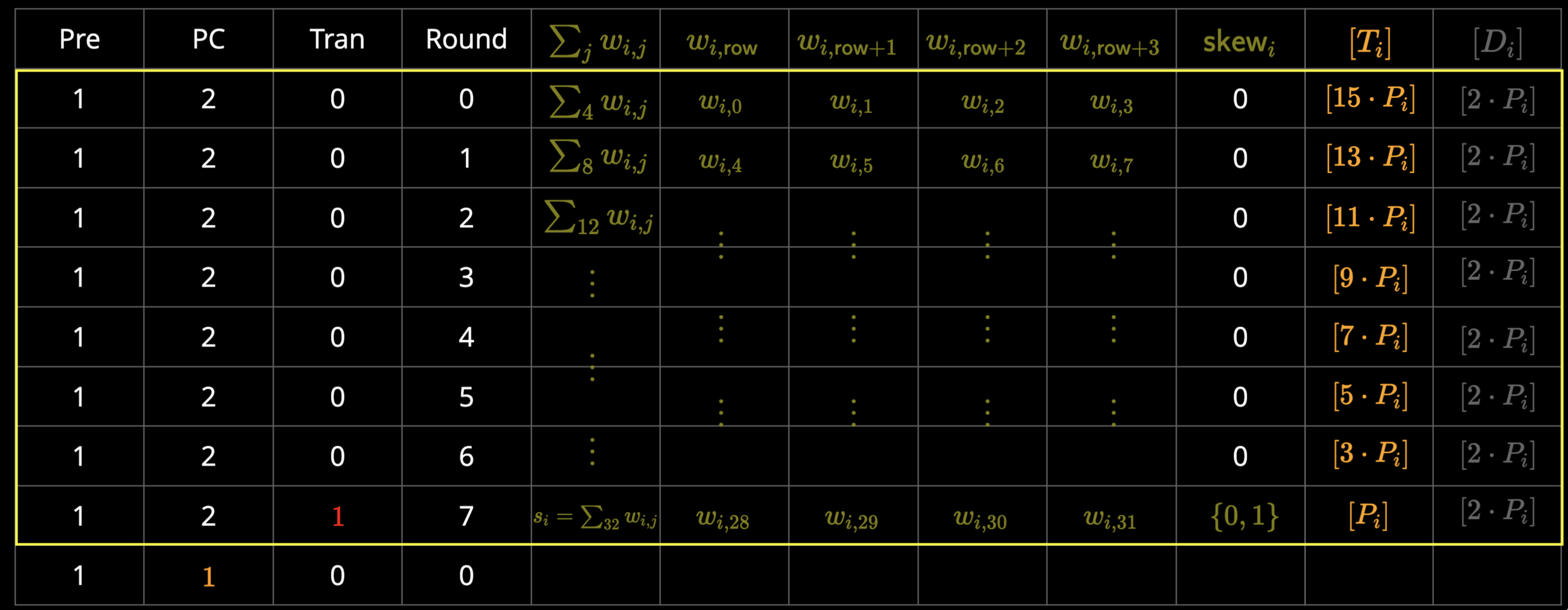
MSM in ECCVM
\begin{aligned}
\implies A = \sum_{i=1}^{m}
\left(
\sum_{j=0}^{31} \textcolor{olive}{w_{i,j}}\cdot\textcolor{orange}{[2^{4j} \cdot P_i]}
- \textcolor{olive}{\textsf{skew}_i}\cdot\textcolor{orange}{[P_i]}
\right)
\end{aligned}
\begin{aligned}
\textcolor{olive}{s_1}\cdot \textcolor{orange}{P_1} \\[5pt]
+\ \textcolor{olive}{s_2}\cdot \textcolor{orange}{P_2} \\[5pt]
+\ \textcolor{olive}{s_3}\cdot \textcolor{orange}{P_3} \\[5pt]
+\ \textcolor{olive}{s_4}\cdot \textcolor{orange}{P_4} \\[5pt]
+\ \textcolor{olive}{s_5}\cdot \textcolor{orange}{P_5} \\[5pt]
+\ \textcolor{olive}{s_6}\cdot \textcolor{orange}{P_6} \\[5pt]
+\ \textcolor{olive}{s_7}\cdot \textcolor{orange}{P_7} \\[5pt]
\end{aligned}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{1,31}}\cdot \textcolor{orange}{P_1}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{1,2}}\cdot \textcolor{orange}{P_1}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{1,1}}\cdot \textcolor{orange}{P_1}\Big]
& + &
\Big[\textcolor{olive}{w_{1,0}} \cdot \textcolor{orange}{P_1}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_1} \cdot \textcolor{orange}{P_1}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{2,31}}\cdot \textcolor{orange}{P_2}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{2,2}}\cdot \textcolor{orange}{P_2}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{2,1}}\cdot \textcolor{orange}{P_2}\Big]
& + &
\Big[\textcolor{olive}{w_{2,0}} \cdot \textcolor{orange}{P_2}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_2} \cdot \textcolor{orange}{P_2}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{3,31}}\cdot \textcolor{orange}{P_3}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{3,2}}\cdot \textcolor{orange}{P_3}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{3,1}}\cdot \textcolor{orange}{P_3}\Big]
& + &
\Big[\textcolor{olive}{w_{3,0}} \cdot \textcolor{orange}{P_3}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_3} \cdot \textcolor{orange}{P_3}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{4,31}}\cdot \textcolor{orange}{P_4}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{4,2}}\cdot \textcolor{orange}{P_4}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{4,1}}\cdot \textcolor{orange}{P_4}\Big]
& + &
\Big[\textcolor{olive}{w_{4,0}} \cdot \textcolor{orange}{P_4}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_4} \cdot \textcolor{orange}{P_4}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{5,31}}\cdot \textcolor{orange}{P_5}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{5,2}}\cdot \textcolor{orange}{P_5}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{5,1}}\cdot \textcolor{orange}{P_5}\Big]
& + &
\Big[\textcolor{olive}{w_{5,0}} \cdot \textcolor{orange}{P_5}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_5} \cdot \textcolor{orange}{P_5}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{6,31}}\cdot \textcolor{orange}{P_6}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{6,2}}\cdot \textcolor{orange}{P_6}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{6,1}}\cdot \textcolor{orange}{P_6}\Big]
& + &
\Big[\textcolor{olive}{w_{6,0}} \cdot \textcolor{orange}{P_6}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_6} \cdot \textcolor{orange}{P_6}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{7,31}}\cdot \textcolor{orange}{P_7}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{7,2}}\cdot \textcolor{orange}{P_7}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{7,1}}\cdot \textcolor{orange}{P_7}\Big]
& + &
\Big[\textcolor{olive}{w_{7,0}} \cdot \textcolor{orange}{P_7}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_7} \cdot \textcolor{orange}{P_7}\Big]
\end{matrix}
A =
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{grey}{0}\cdot \textcolor{grey}{P_7}\Big]
& \ \ & + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{grey}{0}\cdot \textcolor{grey}{P_7}\Big]
& & \ + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{grey}{0}\cdot \textcolor{grey}{P_7}\Big]
& \quad \ + &
\Big[\textcolor{grey}{0} \cdot \textcolor{grey}{P_7}\Big]
& \quad - &
\Big[\textcolor{grey}{0} \cdot \textcolor{grey}{P_7}\Big]
\end{matrix}
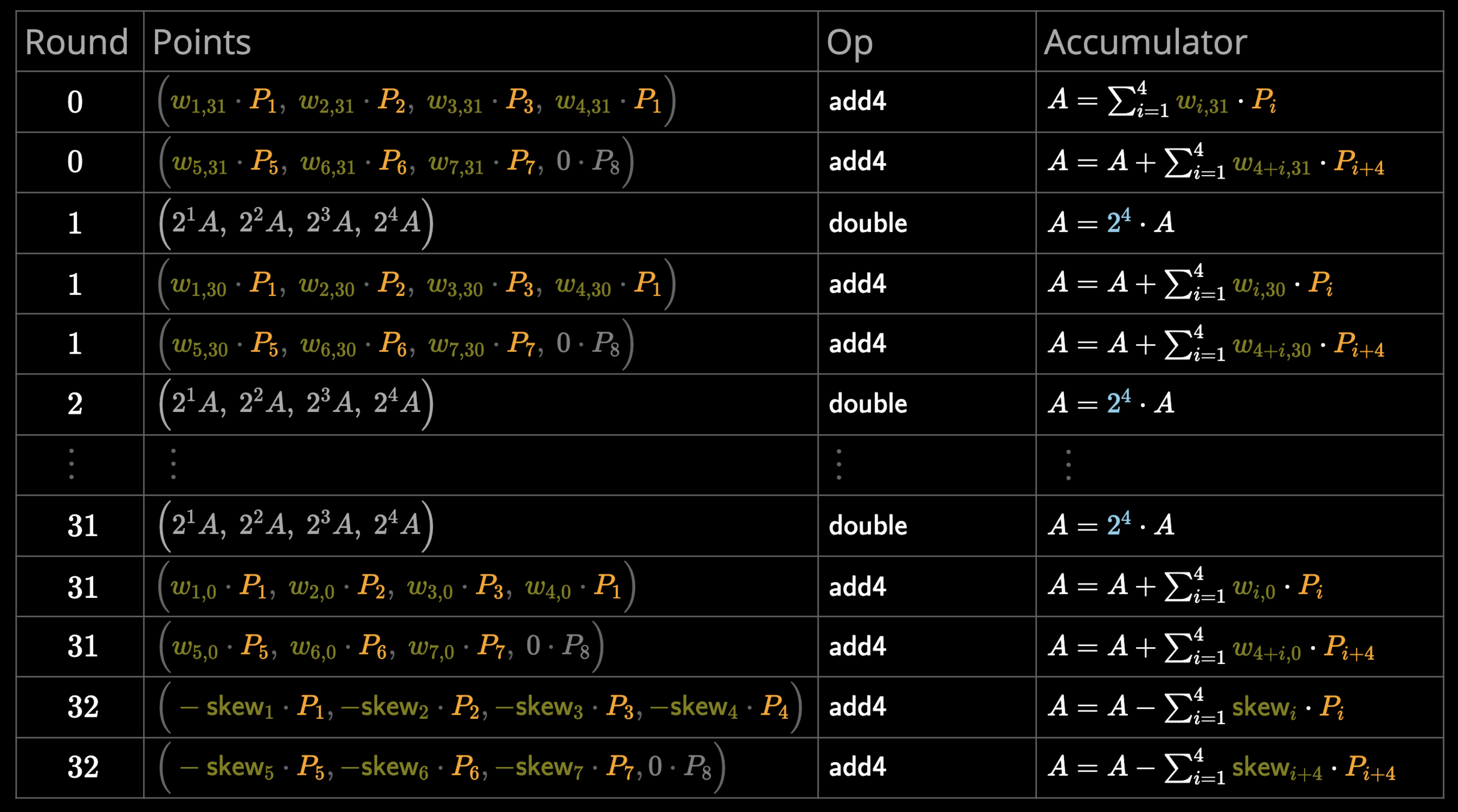
| Round | Points | Op | Accumulator |
0
\Big(
\textcolor{olive}{w_{1,31}}\cdot \textcolor{orange}{P_1},\
\textcolor{olive}{w_{2,31}}\cdot \textcolor{orange}{P_2},\
\textcolor{olive}{w_{3,31}}\cdot \textcolor{orange}{P_3},\
\textcolor{olive}{w_{4,31}}\cdot \textcolor{orange}{P_1}
\Big)
A =
\sum_{i=1}^{4}
\textcolor{olive}{w_{i,31}}\cdot \textcolor{orange}{P_i}
\textsf{add4}
MSM in ECCVM
\begin{aligned}
\textcolor{olive}{s_1}\cdot \textcolor{orange}{P_1} \\[5pt]
+\ \textcolor{olive}{s_2}\cdot \textcolor{orange}{P_2} \\[5pt]
+\ \textcolor{olive}{s_3}\cdot \textcolor{orange}{P_3} \\[5pt]
+\ \textcolor{olive}{s_4}\cdot \textcolor{orange}{P_4} \\[5pt]
+\ \textcolor{olive}{s_5}\cdot \textcolor{orange}{P_5} \\[5pt]
+\ \textcolor{olive}{s_6}\cdot \textcolor{orange}{P_6} \\[5pt]
+\ \textcolor{olive}{s_7}\cdot \textcolor{orange}{P_7} \\[5pt]
\end{aligned}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{1,31}}\cdot \textcolor{orange}{P_1}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{1,2}}\cdot \textcolor{orange}{P_1}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{1,1}}\cdot \textcolor{orange}{P_1}\Big]
& + &
\Big[\textcolor{olive}{w_{1,0}} \cdot \textcolor{orange}{P_1}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_1} \cdot \textcolor{orange}{P_1}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{2,31}}\cdot \textcolor{orange}{P_2}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{2,2}}\cdot \textcolor{orange}{P_2}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{2,1}}\cdot \textcolor{orange}{P_2}\Big]
& + &
\Big[\textcolor{olive}{w_{2,0}} \cdot \textcolor{orange}{P_2}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_2} \cdot \textcolor{orange}{P_2}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{3,31}}\cdot \textcolor{orange}{P_3}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{3,2}}\cdot \textcolor{orange}{P_3}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{3,1}}\cdot \textcolor{orange}{P_3}\Big]
& + &
\Big[\textcolor{olive}{w_{3,0}} \cdot \textcolor{orange}{P_3}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_3} \cdot \textcolor{orange}{P_3}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{4,31}}\cdot \textcolor{orange}{P_4}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{4,2}}\cdot \textcolor{orange}{P_4}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{4,1}}\cdot \textcolor{orange}{P_4}\Big]
& + &
\Big[\textcolor{olive}{w_{4,0}} \cdot \textcolor{orange}{P_4}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_4} \cdot \textcolor{orange}{P_4}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{5,31}}\cdot \textcolor{orange}{P_5}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{5,2}}\cdot \textcolor{orange}{P_5}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{5,1}}\cdot \textcolor{orange}{P_5}\Big]
& + &
\Big[\textcolor{olive}{w_{5,0}} \cdot \textcolor{orange}{P_5}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_5} \cdot \textcolor{orange}{P_5}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{6,31}}\cdot \textcolor{orange}{P_6}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{6,2}}\cdot \textcolor{orange}{P_6}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{6,1}}\cdot \textcolor{orange}{P_6}\Big]
& + &
\Big[\textcolor{olive}{w_{6,0}} \cdot \textcolor{orange}{P_6}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_6} \cdot \textcolor{orange}{P_6}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{7,31}}\cdot \textcolor{orange}{P_7}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{7,2}}\cdot \textcolor{orange}{P_7}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{7,1}}\cdot \textcolor{orange}{P_7}\Big]
& + &
\Big[\textcolor{olive}{w_{7,0}} \cdot \textcolor{orange}{P_7}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_7} \cdot \textcolor{orange}{P_7}\Big]
\end{matrix}
A =
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}\Big]
& \ \ & + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}\Big]
& & \ + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}\Big]
& \quad \ + &
\Big[\textcolor{grey}{0} \cdot \textcolor{grey}{P_8}\Big]
& \quad - &
\Big[\textcolor{grey}{0} \cdot \textcolor{grey}{P_8}\Big]
\end{matrix}
| Round | Points | Op | Accumulator |
0
\Big(
\textcolor{olive}{w_{1,31}}\cdot \textcolor{orange}{P_1},\
\textcolor{olive}{w_{2,31}}\cdot \textcolor{orange}{P_2},\
\textcolor{olive}{w_{3,31}}\cdot \textcolor{orange}{P_3},\
\textcolor{olive}{w_{4,31}}\cdot \textcolor{orange}{P_1}
\Big)
A =
\sum_{i=1}^{4}
\textcolor{olive}{w_{i,31}}\cdot \textcolor{orange}{P_i}
\textsf{add4}
MSM in ECCVM
\begin{aligned}
\textcolor{olive}{s_1}\cdot \textcolor{orange}{P_1} \\[5pt]
+\ \textcolor{olive}{s_2}\cdot \textcolor{orange}{P_2} \\[5pt]
+\ \textcolor{olive}{s_3}\cdot \textcolor{orange}{P_3} \\[5pt]
+\ \textcolor{olive}{s_4}\cdot \textcolor{orange}{P_4} \\[5pt]
+\ \textcolor{olive}{s_5}\cdot \textcolor{orange}{P_5} \\[5pt]
+\ \textcolor{olive}{s_6}\cdot \textcolor{orange}{P_6} \\[5pt]
+\ \textcolor{olive}{s_7}\cdot \textcolor{orange}{P_7} \\[5pt]
\end{aligned}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{1,31}}\cdot \textcolor{orange}{P_1}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{1,2}}\cdot \textcolor{orange}{P_1}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{1,1}}\cdot \textcolor{orange}{P_1}\Big]
& + &
\Big[\textcolor{olive}{w_{1,0}} \cdot \textcolor{orange}{P_1}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_1} \cdot \textcolor{orange}{P_1}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{2,31}}\cdot \textcolor{orange}{P_2}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{2,2}}\cdot \textcolor{orange}{P_2}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{2,1}}\cdot \textcolor{orange}{P_2}\Big]
& + &
\Big[\textcolor{olive}{w_{2,0}} \cdot \textcolor{orange}{P_2}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_2} \cdot \textcolor{orange}{P_2}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{3,31}}\cdot \textcolor{orange}{P_3}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{3,2}}\cdot \textcolor{orange}{P_3}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{3,1}}\cdot \textcolor{orange}{P_3}\Big]
& + &
\Big[\textcolor{olive}{w_{3,0}} \cdot \textcolor{orange}{P_3}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_3} \cdot \textcolor{orange}{P_3}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{4,31}}\cdot \textcolor{orange}{P_4}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{4,2}}\cdot \textcolor{orange}{P_4}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{4,1}}\cdot \textcolor{orange}{P_4}\Big]
& + &
\Big[\textcolor{olive}{w_{4,0}} \cdot \textcolor{orange}{P_4}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_4} \cdot \textcolor{orange}{P_4}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{5,31}}\cdot \textcolor{orange}{P_5}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{5,2}}\cdot \textcolor{orange}{P_5}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{5,1}}\cdot \textcolor{orange}{P_5}\Big]
& + &
\Big[\textcolor{olive}{w_{5,0}} \cdot \textcolor{orange}{P_5}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_5} \cdot \textcolor{orange}{P_5}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{6,31}}\cdot \textcolor{orange}{P_6}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{6,2}}\cdot \textcolor{orange}{P_6}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{6,1}}\cdot \textcolor{orange}{P_6}\Big]
& + &
\Big[\textcolor{olive}{w_{6,0}} \cdot \textcolor{orange}{P_6}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_6} \cdot \textcolor{orange}{P_6}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{7,31}}\cdot \textcolor{orange}{P_7}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{7,2}}\cdot \textcolor{orange}{P_7}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{7,1}}\cdot \textcolor{orange}{P_7}\Big]
& + &
\Big[\textcolor{olive}{w_{7,0}} \cdot \textcolor{orange}{P_7}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_7} \cdot \textcolor{orange}{P_7}\Big]
\end{matrix}
A =
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}\Big]
& \ \ & + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}\Big]
& & \ + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}\Big]
& \quad \ + &
\Big[\textcolor{grey}{0} \cdot \textcolor{grey}{P_8}\Big]
& \quad - &
\Big[\textcolor{grey}{0} \cdot \textcolor{grey}{P_8}\Big]
\end{matrix}
| Round | Points | Op | Accumulator |
0
\Big(
\textcolor{olive}{w_{1,31}}\cdot \textcolor{orange}{P_1},\
\textcolor{olive}{w_{2,31}}\cdot \textcolor{orange}{P_2},\
\textcolor{olive}{w_{3,31}}\cdot \textcolor{orange}{P_3},\
\textcolor{olive}{w_{4,31}}\cdot \textcolor{orange}{P_1}
\Big)
A =
\sum_{i=1}^{4}
\textcolor{olive}{w_{i,31}}\cdot \textcolor{orange}{P_i}
\textsf{add4}
0
\Big(
\textcolor{olive}{w_{5,31}}\cdot \textcolor{orange}{P_5},\
\textcolor{olive}{w_{6,31}}\cdot \textcolor{orange}{P_6},\
\textcolor{olive}{w_{7,31}}\cdot \textcolor{orange}{P_7},\
\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}
\Big)
\textsf{add4}
A = A + \sum_{i=1}^{4}
\textcolor{olive}{w_{4 + i,31}}\cdot \textcolor{orange}{P_{i+4}}
MSM in ECCVM
\begin{aligned}
\textcolor{olive}{s_1}\cdot \textcolor{orange}{P_1} \\[5pt]
+\ \textcolor{olive}{s_2}\cdot \textcolor{orange}{P_2} \\[5pt]
+\ \textcolor{olive}{s_3}\cdot \textcolor{orange}{P_3} \\[5pt]
+\ \textcolor{olive}{s_4}\cdot \textcolor{orange}{P_4} \\[5pt]
+\ \textcolor{olive}{s_5}\cdot \textcolor{orange}{P_5} \\[5pt]
+\ \textcolor{olive}{s_6}\cdot \textcolor{orange}{P_6} \\[5pt]
+\ \textcolor{olive}{s_7}\cdot \textcolor{orange}{P_7} \\[5pt]
\end{aligned}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{1,31}}\cdot \textcolor{orange}{P_1}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{1,2}}\cdot \textcolor{orange}{P_1}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{1,1}}\cdot \textcolor{orange}{P_1}\Big]
& + &
\Big[\textcolor{olive}{w_{1,0}} \cdot \textcolor{orange}{P_1}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_1} \cdot \textcolor{orange}{P_1}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{2,31}}\cdot \textcolor{orange}{P_2}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{2,2}}\cdot \textcolor{orange}{P_2}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{2,1}}\cdot \textcolor{orange}{P_2}\Big]
& + &
\Big[\textcolor{olive}{w_{2,0}} \cdot \textcolor{orange}{P_2}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_2} \cdot \textcolor{orange}{P_2}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{3,31}}\cdot \textcolor{orange}{P_3}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{3,2}}\cdot \textcolor{orange}{P_3}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{3,1}}\cdot \textcolor{orange}{P_3}\Big]
& + &
\Big[\textcolor{olive}{w_{3,0}} \cdot \textcolor{orange}{P_3}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_3} \cdot \textcolor{orange}{P_3}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{4,31}}\cdot \textcolor{orange}{P_4}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{4,2}}\cdot \textcolor{orange}{P_4}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{4,1}}\cdot \textcolor{orange}{P_4}\Big]
& + &
\Big[\textcolor{olive}{w_{4,0}} \cdot \textcolor{orange}{P_4}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_4} \cdot \textcolor{orange}{P_4}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{5,31}}\cdot \textcolor{orange}{P_5}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{5,2}}\cdot \textcolor{orange}{P_5}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{5,1}}\cdot \textcolor{orange}{P_5}\Big]
& + &
\Big[\textcolor{olive}{w_{5,0}} \cdot \textcolor{orange}{P_5}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_5} \cdot \textcolor{orange}{P_5}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{6,31}}\cdot \textcolor{orange}{P_6}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{6,2}}\cdot \textcolor{orange}{P_6}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{6,1}}\cdot \textcolor{orange}{P_6}\Big]
& + &
\Big[\textcolor{olive}{w_{6,0}} \cdot \textcolor{orange}{P_6}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_6} \cdot \textcolor{orange}{P_6}\Big]
\end{matrix}
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{olive}{w_{7,31}}\cdot \textcolor{orange}{P_7}\Big]
& + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{olive}{w_{7,2}}\cdot \textcolor{orange}{P_7}\Big]
& + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{olive}{w_{7,1}}\cdot \textcolor{orange}{P_7}\Big]
& + &
\Big[\textcolor{olive}{w_{7,0}} \cdot \textcolor{orange}{P_7}\Big]
& - &
\Big[\textcolor{olive}{\textsf{skew}_7} \cdot \textcolor{orange}{P_7}\Big]
\end{matrix}
A =
\begin{matrix}
\textcolor{skyblue}{2^{124}} * \Big[\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}\Big]
& \ \ & + &
\dots
& + &
\textcolor{skyblue}{2^8} * \Big[\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}\Big]
& & \ + &
\textcolor{skyblue}{2^4} * \Big[\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}\Big]
& \quad \ + &
\Big[\textcolor{grey}{0} \cdot \textcolor{grey}{P_8}\Big]
& \quad - &
\Big[\textcolor{grey}{0} \cdot \textcolor{grey}{P_8}\Big]
\end{matrix}
| Round | Points | Op | Accumulator |
0
\Big(
\textcolor{olive}{w_{1,31}}\cdot \textcolor{orange}{P_1},\
\textcolor{olive}{w_{2,31}}\cdot \textcolor{orange}{P_2},\
\textcolor{olive}{w_{3,31}}\cdot \textcolor{orange}{P_3},\
\textcolor{olive}{w_{4,31}}\cdot \textcolor{orange}{P_1}
\Big)
A =
\sum_{i=1}^{4}
\textcolor{olive}{w_{i,31}}\cdot \textcolor{orange}{P_i}
\textsf{add4}
0
\Big(
\textcolor{olive}{w_{5,31}}\cdot \textcolor{orange}{P_5},\
\textcolor{olive}{w_{6,31}}\cdot \textcolor{orange}{P_6},\
\textcolor{olive}{w_{7,31}}\cdot \textcolor{orange}{P_7},\
\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}
\Big)
\textsf{add4}
A = A + \sum_{i=1}^{4}
\textcolor{olive}{w_{4 + i,31}}\cdot \textcolor{orange}{P_{i+4}}
1
\Big(
2^1A, \ 2^2A, \ 2^3A, \ 2^4A
\Big)
\textsf{double}
A = \textcolor{skyblue}{2^4}\cdot A
MSM in ECCVM
| Round | Points | Op | Accumulator |
0
\Big(
\textcolor{olive}{w_{1,31}}\cdot \textcolor{orange}{P_1},\
\textcolor{olive}{w_{2,31}}\cdot \textcolor{orange}{P_2},\
\textcolor{olive}{w_{3,31}}\cdot \textcolor{orange}{P_3},\
\textcolor{olive}{w_{4,31}}\cdot \textcolor{orange}{P_1}
\Big)
A =
\sum_{i=1}^{4}
\textcolor{olive}{w_{i,31}}\cdot \textcolor{orange}{P_i}
\textsf{add4}
0
\Big(
\textcolor{olive}{w_{5,31}}\cdot \textcolor{orange}{P_5},\
\textcolor{olive}{w_{6,31}}\cdot \textcolor{orange}{P_6},\
\textcolor{olive}{w_{7,31}}\cdot \textcolor{orange}{P_7},\
\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}
\Big)
\textsf{add4}
A = A + \sum_{i=1}^{4}
\textcolor{olive}{w_{4 + i,31}}\cdot \textcolor{orange}{P_{i+4}}
1
\Big(
2^1A, \ 2^2A, \ 2^3A, \ 2^4A
\Big)
\textsf{double}
A = \textcolor{skyblue}{2^4}\cdot A
1
\Big(
\textcolor{olive}{w_{1,30}}\cdot \textcolor{orange}{P_1},\
\textcolor{olive}{w_{2,30}}\cdot \textcolor{orange}{P_2},\
\textcolor{olive}{w_{3,30}}\cdot \textcolor{orange}{P_3},\
\textcolor{olive}{w_{4,30}}\cdot \textcolor{orange}{P_1}
\Big)
A = A +
\sum_{i=1}^{4}
\textcolor{olive}{w_{i,30}}\cdot \textcolor{orange}{P_i}
\textsf{add4}
1
\Big(
\textcolor{olive}{w_{5,30}}\cdot \textcolor{orange}{P_5},\
\textcolor{olive}{w_{6,30}}\cdot \textcolor{orange}{P_6},\
\textcolor{olive}{w_{7,30}}\cdot \textcolor{orange}{P_7},\
\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}
\Big)
\textsf{add4}
A = A + \sum_{i=1}^{4}
\textcolor{olive}{w_{4 + i,30}}\cdot \textcolor{orange}{P_{i+4}}
2
\Big(
2^1A, \ 2^2A, \ 2^3A, \ 2^4A
\Big)
\textsf{double}
A = \textcolor{skyblue}{2^4}\cdot A
\vdots
\vdots
\vdots
\vdots
31
\Big(
2^1A, \ 2^2A, \ 2^3A, \ 2^4A
\Big)
\textsf{double}
A = \textcolor{skyblue}{2^4}\cdot A
31
\Big(
\textcolor{olive}{w_{1,0}}\cdot \textcolor{orange}{P_1},\
\textcolor{olive}{w_{2,0}}\cdot \textcolor{orange}{P_2},\
\textcolor{olive}{w_{3,0}}\cdot \textcolor{orange}{P_3},\
\textcolor{olive}{w_{4,0}}\cdot \textcolor{orange}{P_1}
\Big)
A = A +
\sum_{i=1}^{4}
\textcolor{olive}{w_{i,0}}\cdot \textcolor{orange}{P_i}
\textsf{add4}
31
\Big(
\textcolor{olive}{w_{5,0}}\cdot \textcolor{orange}{P_5},\
\textcolor{olive}{w_{6,0}}\cdot \textcolor{orange}{P_6},\
\textcolor{olive}{w_{7,0}}\cdot \textcolor{orange}{P_7},\
\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}
\Big)
\textsf{add4}
A = A + \sum_{i=1}^{4}
\textcolor{olive}{w_{4 + i,0}}\cdot \textcolor{orange}{P_{i+4}}
32
\Big(
\textcolor{olive}{-\textsf{skew}_1}\cdot \textcolor{orange}{P_1},
\textcolor{olive}{-\textsf{skew}_2}\cdot \textcolor{orange}{P_2},
\textcolor{olive}{-\textsf{skew}_3}\cdot \textcolor{orange}{P_3},
\textcolor{olive}{-\textsf{skew}_4}\cdot \textcolor{orange}{P_4}
\Big)
\textsf{add4}
A = A - \sum_{i=1}^{4}
\textcolor{olive}{\textsf{skew}_{i}}\cdot \textcolor{orange}{P_{i}}
32
\Big(
\textcolor{olive}{-\textsf{skew}_5}\cdot \textcolor{orange}{P_5},
\textcolor{olive}{-\textsf{skew}_6}\cdot \textcolor{orange}{P_6},
\textcolor{olive}{-\textsf{skew}_7}\cdot \textcolor{orange}{P_7},
\textcolor{grey}{0}\cdot \textcolor{grey}{P_8}
\Big)
\textsf{add4}
A = A - \sum_{i=1}^{4}
\textcolor{olive}{\textsf{skew}_{i+4}}\cdot \textcolor{orange}{P_{i+4}}
ECCVM Gate Count
- Let's say we need to perform an MSM of size \(M\)
- We can calculate the no. of rows for three table types:
- MSM table:
- \(N_{\textsf{msm}} = \left(\left\lceil\frac{M}{4}\right\rceil + 1\right) \times \left(\frac{128}{w} + 1\right) - 2\)
- Pre-computation table:
- \(N_{\textsf{pre}} = M \times \frac{128}{w\times 4}\)
- Transcript table:
- \(N_{\textsf{trc}} \le M \times 3\)
- MSM table:
- The overall gate-count would be:
N = \textsf{max}(N_{\textsf{msm}}, N_{\textsf{pre}}, N_{\textsf{trc}})
ECCVM Relations
- Defining trace tables and their structures isn't enough
- We need to prove that certain mathematical relations hold in the trace tables

\textsf{pc}_{i} - \textsf{pc}_{i+1} = (z_{1,i} \neq 0 \ + \ z_{2,i} \neq 0)
ECCVM Relations
- Defining trace tables and their structures isn't enough
- We need to prove that certain mathematical relations hold in the trace tables

M_i = M_{i-1} + (z_{1,i}\cdot \textcolor{orange}{P_i} + z_{2,i}\cdot \textcolor{orange}{\lambda P_i})
ECCVM Relations
- Defining trace tables and their structures isn't enough
- We need to prove that certain mathematical relations hold in the trace tables
w_{\text{sum}, i+1} - 2^{16}w_{\text{sum}, i} = \sum_{k=1}^{4} 2^{4j} \cdot w_{i, k}
ECCVM Relations
- Defining trace tables and their structures isn't enough
- We need to prove that certain mathematical relations hold in the trace tables
Lookup relation with pre-computation table
References
- Original ECCVM specification
- \(w\)NAF documentation
- Pedersen hashing in TurboPlonk using \(w\)NAF: specification