Plonk Optimisations
Aztec Study Club - Session 9
11th May 2022
Plonk Constraints
StandardPlonk
TurboPlonk
Width = \(4\)
Circuit size = \(n\)
Copy constraints
Cell-wise permutation
Plonk Costs
Width = \(4\)
Circuit size = \(n\)
\(x\)
\(y\)
\(1\)
\(\omega\)
\(\omega^2\)
\(\omega^4\)
\(\omega^5\)
\(\omega^6\)
\(\omega^7\)
\(\omega^3\)
Plonk Optimisations
Width = \(4\)
Circuit size = \(n\)
- Prover work of any zk-SNARK is primarily: FFTs and MSMs
- FFTs are \(\mathcal{O}(n \ \text{log}(n))\)
- MSMs are \(\mathcal{O}(n / \text{log}(n))\)
- But a single MSM is \(\approx 5\times\) more expensive than an FFT
- How do we optimise prover costs?
- Simple! Reduce the circuit size \(n\)
- TurboPLONK: custom gate to do complex operations more than just addition and multiplication
- UltraPLONK: use lookup tables to efficiently do bitwise operations
- Honk teaser: can we get rid of FFTs completely? 😉
Plonk Optimisations ft. ZCash
Width = \(4\)
Circuit size = \(n\)
- TurboPLONK means more computation per gate
- This means fewer total number of gates!
- On the same lines, can we increase the width?
Plonk Optimisations ft. ZCash
Width = \(4\)
Circuit size = \(n\)
- TurboPLONK means more computation per gate
- This means fewer total number of gates!
- On the same lines, can we increase the width?
Plonk Optimisations ft. ZCash
Width = \(6\)
Circuit size = \(n\)
- TurboPLONK means more computation per gate
- This means fewer total number of gates!
- On the same lines, can we increase the width?
Plonk Optimisations ft. ZCash
Width = \(6\)
Circuit size = \(n' < n\)
- TurboPLONK means more computation per gate
- This means fewer total number of gates!
- On the same lines, can we increase the width?
- Indeed, increasing width reduces circuit size!
- Wait, what's the tradeoff?
- So more the no of columns, more the MSMs
Plonk Optimisations ft. ZCash
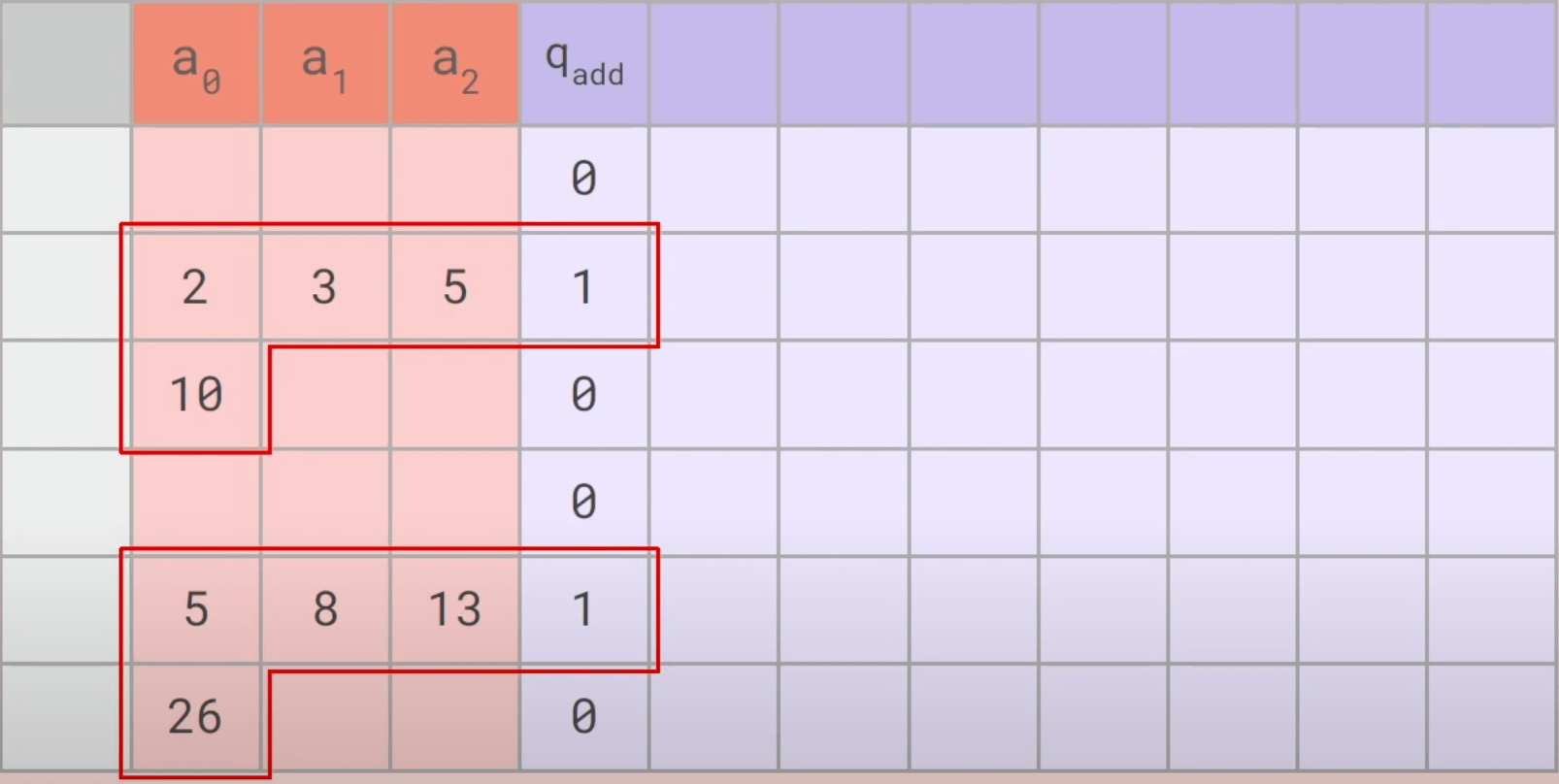
Credit: ZK7: Latest developments in Halo2 by Ying Tong Lai 🔗
empty wire values
Plonk Optimisations ft. ZCash
Credit: ZK7: Latest developments in Halo2 by Ying Tong Lai 🔗

empty spaces
Layouting
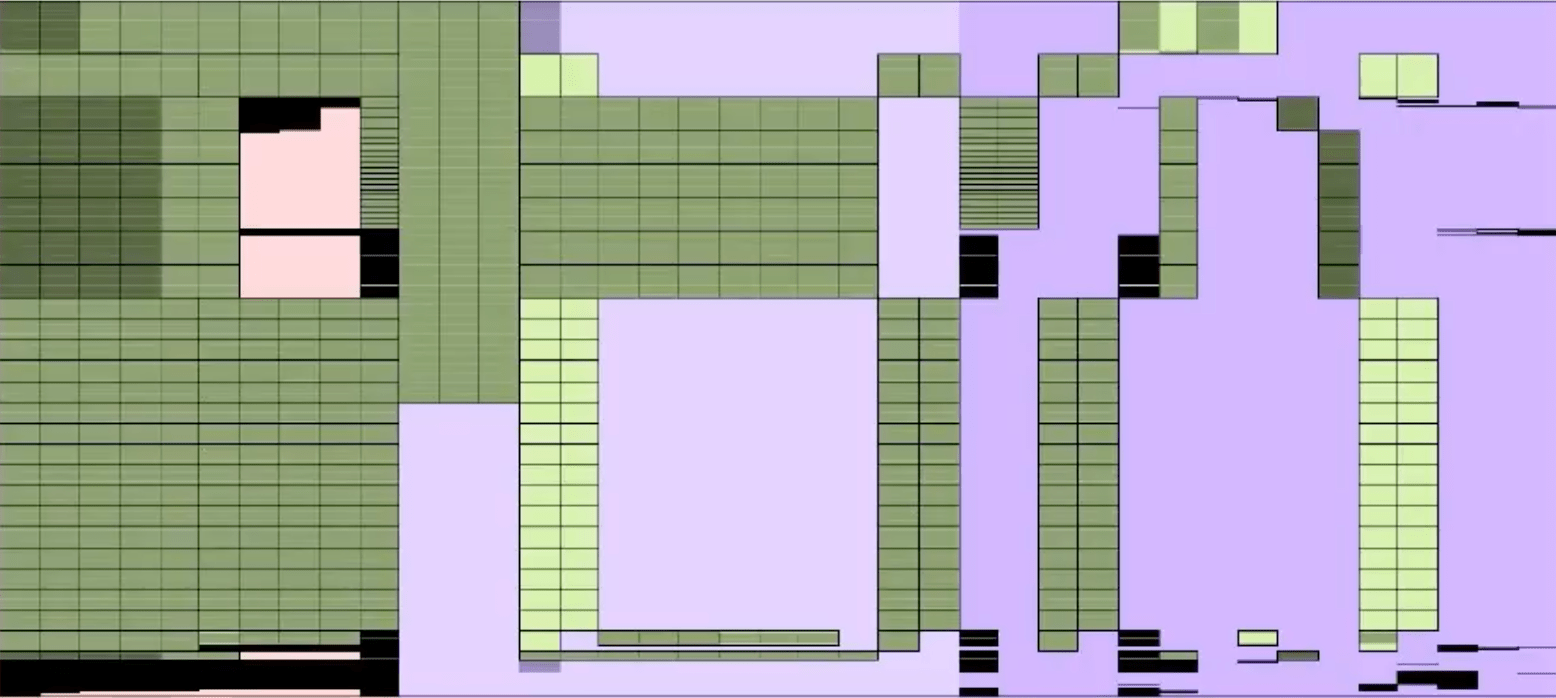

width \(= 2^{12}\)
width \(= 2^{11}\)
Credit: ZK7: Latest developments in Halo2 by Ying Tong Lai 🔗
Omnipresent Plonk

TurboPlonk for scaling on Ethereum

TurboPlonk + FRI for scaling on Ethereum

UltraPlonk + recursion to build a 5kb blockchain

UltraPlonk + Bulletproofs = Halo2

UltraPlonk (they call is PlonkUp) for RegDeFi (?)

Optimized Poseidon using TurboPlonk for zkRollup on Tezos