Plookup & Plonk
Aztec Study Club - Session 8
28th April 2022
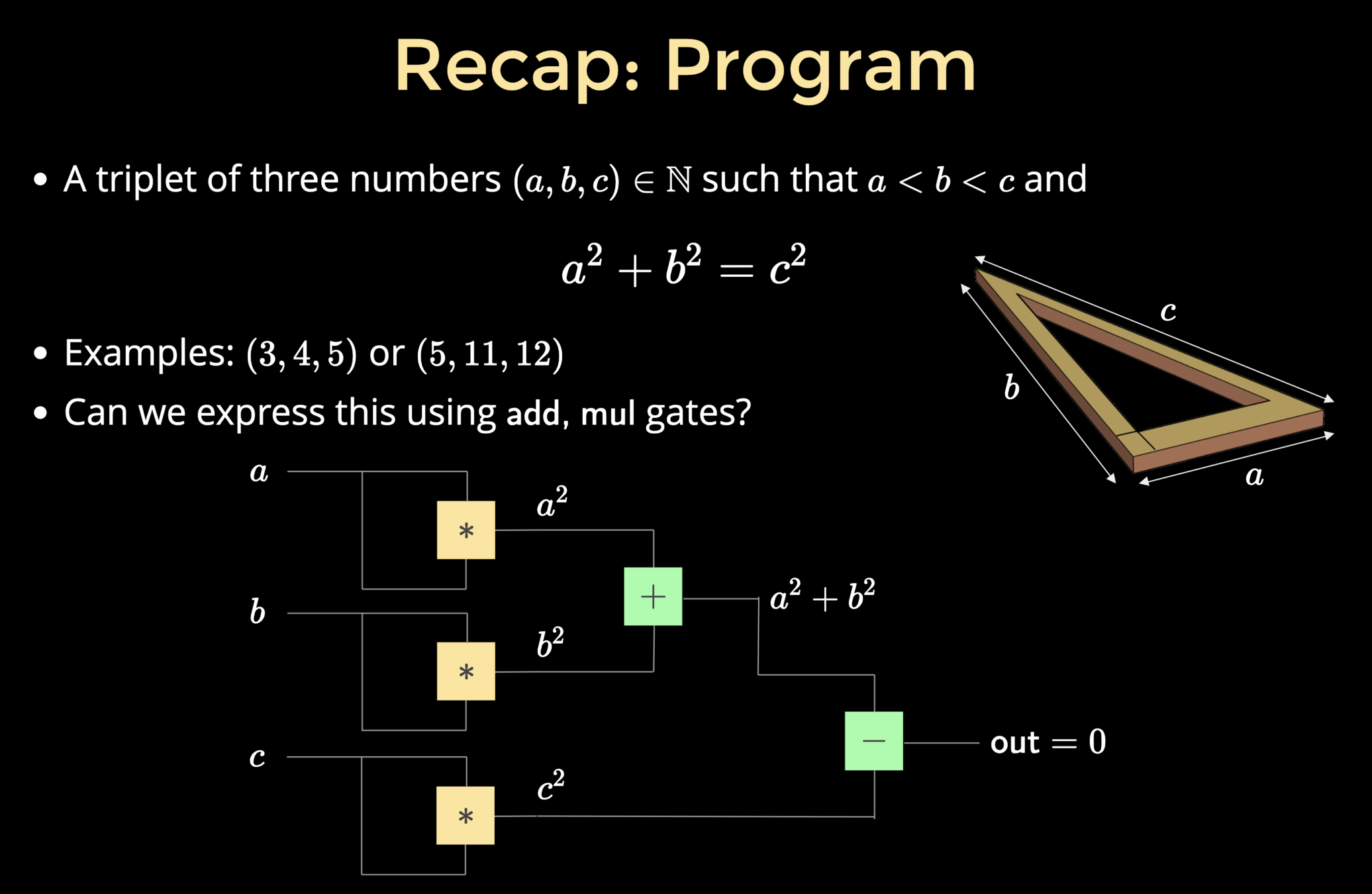
Recap: Program
- A triplet of three numbers \((a, b, c) \in \mathbb{N}\) such that \(a < b < c\) and
a^2+b^2=c^2
- Examples: \((3,4,5)\) or \((5,11,12)\)
- Can we express this using \(\textsf{add, mul}\) gates?

b
c
a
a
\(\ast\)
b
\(\ast\)
c
\(\ast\)
\(+\)
\(-\)
\textsf{out} = 0
a^2
b^2
c^2
a^2+b^2
Recap: Constraints
x_1
\(\ast\)
x_2
\(\ast\)
x_3
\(\ast\)
\(+\)
x_4
x_5
x_6
- Each gate has three wires: \(w_l, w_r, w_o\)
\textcolor{gray}{0\cdot} x_1 + \textcolor{gray}{0\cdot}x_1 + \textcolor{gray}{1\cdot}(x_1x_1) \textcolor{gray}{-1\cdot}x_4 + \textcolor{gray}{0} = 0
\textcolor{gray}{1\cdot}x_4 + \textcolor{gray}{1\cdot}x_5 + \textcolor{gray}{0\cdot}(x_4x_5) \textcolor{gray}{-1\cdot}x_6 + 0 = 0
1
2
3
4
x_1
x_1
x_4
x_1^2 = x_4
x_2
x_2
x_5
x_2^2=x_5
x_3
x_3
x_6
x_3^2=x_6
x_4
x_5
x_6
x_4+x_5=x_6
\textcolor{gray}{0\cdot} x_2 + \textcolor{gray}{0\cdot}x_2 + \textcolor{gray}{1\cdot}(x_2x_2) \textcolor{gray}{-1\cdot}x_5 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_3 + \textcolor{gray}{0\cdot}x_3 + \textcolor{gray}{1\cdot}(x_3x_3) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
- Gate constraint: \(\textcolor{gray}{q_l\cdot}w_l + \textcolor{gray}{q_r\cdot}w_r + \textcolor{gray}{q_m\cdot}w_lw_r + \textcolor{gray}{q_o\cdot}w_o + \textcolor{gray}{q_c} = 0\)
w_l
w_r
w_o
\text{Constraint}
i
Selectors
Witnesses
Recap: Constraints
x_1
\(\ast\)
x_2
\(\ast\)
x_3
\(\ast\)
\(+\)
x_4
x_5
x_6
- Each gate has three wires: \(w_l, w_r, w_o\)
1
2
3
4
x_1
x_1
x_4
x_1^2 = x_4
x_2
x_2
x_5
x_2^2=x_5
x_3
x_3
x_6
x_3^2=x_6
x_4
x_5
x_6
x_4+x_5=x_6
- Copy constraints:
w_l
w_r
w_o
\text{Constraint}
i
\begin{aligned}
(w_{o})_1 = (w_l)_4 \\[5pt]
(w_{o})_2 = (w_r)_4 \\[5pt]
(w_{o})_3 = (w_o)_4
\end{aligned}
1
2
3
4
- We can combine gate and copy constraints in a single huge equation!
Recap: Polynomials
- How do we prove the correctness of a set of equations?
\textcolor{gray}{0\cdot} x_1 + \textcolor{gray}{0\cdot}x_1 + \textcolor{gray}{1\cdot}(x_1x_1) \textcolor{gray}{-1\cdot}x_4 + \textcolor{gray}{0} = 0
\textcolor{gray}{1\cdot}x_4 + \textcolor{gray}{1\cdot}x_5 + \textcolor{gray}{0\cdot}(x_4x_5) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_2 + \textcolor{gray}{0\cdot}x_2 + \textcolor{gray}{1\cdot}(x_2x_2) \textcolor{gray}{-1\cdot}x_5 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_3 + \textcolor{gray}{0\cdot}x_3 + \textcolor{gray}{1\cdot}(x_3x_3) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{q_l(X)}w_l(X) + \textcolor{gray}{q_r(X)}w_r(X) + \textcolor{gray}{q_m(X)}w_l(X)w_r(X) + \textcolor{gray}{q_o(X)}w_o(X) + \textcolor{gray}{q_c}(X) = 0
- How do we prove the correctness of a set of equations?
\textcolor{gray}{0\cdot} x_1 + \textcolor{gray}{0\cdot}x_1 + \textcolor{gray}{1\cdot}(x_1x_1) \textcolor{gray}{-1\cdot}x_4 + \textcolor{gray}{0} = 0
\textcolor{gray}{1\cdot}x_4 + \textcolor{gray}{1\cdot}x_5 + \textcolor{gray}{0\cdot}(x_4x_5) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_2 + \textcolor{gray}{0\cdot}x_2 + \textcolor{gray}{1\cdot}(x_2x_2) \textcolor{gray}{-1\cdot}x_5 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_3 + \textcolor{gray}{0\cdot}x_3 + \textcolor{gray}{1\cdot}(x_3x_3) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{q_l(X)}w_l(X) + \textcolor{gray}{q_r(X)}w_r(X) + \textcolor{gray}{q_m(X)}w_l(X)w_r(X) + \textcolor{gray}{q_o(X)}w_o(X) + \textcolor{gray}{q_c}(X) = 0
Recap: Polynomials
- How do we prove the correctness of a set of equations?
\textcolor{gray}{0\cdot} x_1 + \textcolor{gray}{0\cdot}x_1 + \textcolor{gray}{1\cdot}(x_1x_1) \textcolor{gray}{-1\cdot}x_4 + \textcolor{gray}{0} = 0
\textcolor{gray}{1\cdot}x_4 + \textcolor{gray}{1\cdot}x_5 + \textcolor{gray}{0\cdot}(x_4x_5) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_2 + \textcolor{gray}{0\cdot}x_2 + \textcolor{gray}{1\cdot}(x_2x_2) \textcolor{gray}{-1\cdot}x_5 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_3 + \textcolor{gray}{0\cdot}x_3 + \textcolor{gray}{1\cdot}(x_3x_3) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{q_l(X)}w_l(X) + \textcolor{gray}{q_r(X)}w_r(X) + \textcolor{gray}{q_m(X)}w_l(X)w_r(X) + \textcolor{gray}{q_o(X)}w_o(X) + \textcolor{gray}{q_c}(X) = 0
Recap: Polynomials
- How do we prove the correctness of a set of equations?
\textcolor{gray}{0\cdot} x_1 + \textcolor{gray}{0\cdot}x_1 + \textcolor{gray}{1\cdot}(x_1x_1) \textcolor{gray}{-1\cdot}x_4 + \textcolor{gray}{0} = 0
\textcolor{gray}{1\cdot}x_4 + \textcolor{gray}{1\cdot}x_5 + \textcolor{gray}{0\cdot}(x_4x_5) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_2 + \textcolor{gray}{0\cdot}x_2 + \textcolor{gray}{1\cdot}(x_2x_2) \textcolor{gray}{-1\cdot}x_5 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_3 + \textcolor{gray}{0\cdot}x_3 + \textcolor{gray}{1\cdot}(x_3x_3) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{q_l(X)}w_l(X) + \textcolor{gray}{q_r(X)}w_r(X) + \textcolor{gray}{q_m(X)}w_l(X)w_r(X) + \textcolor{gray}{q_o(X)}w_o(X) + \textcolor{gray}{q_c}(X) = 0
Recap: Polynomials
- How do we prove the correctness of a set of equations?
\textcolor{gray}{0\cdot} x_1 + \textcolor{gray}{0\cdot}x_1 + \textcolor{gray}{1\cdot}(x_1x_1) \textcolor{gray}{-1\cdot}x_4 + \textcolor{gray}{0} = 0
\textcolor{gray}{1\cdot}x_4 + \textcolor{gray}{1\cdot}x_5 + \textcolor{gray}{0\cdot}(x_4x_5) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_2 + \textcolor{gray}{0\cdot}x_2 + \textcolor{gray}{1\cdot}(x_2x_2) \textcolor{gray}{-1\cdot}x_5 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_3 + \textcolor{gray}{0\cdot}x_3 + \textcolor{gray}{1\cdot}(x_3x_3) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{q_l(X)}w_l(X) + \textcolor{gray}{q_r(X)}w_r(X) + \textcolor{gray}{q_m(X)}w_l(X)w_r(X) + \textcolor{gray}{q_o(X)}w_o(X) + \textcolor{gray}{q_c}(X) = 0
Recap: Polynomials
- How do we prove the correctness of a set of equations?
\textcolor{gray}{0\cdot} x_1 + \textcolor{gray}{0\cdot}x_1 + \textcolor{gray}{1\cdot}(x_1x_1) \textcolor{gray}{-1\cdot}x_4 + \textcolor{gray}{0} = 0
\textcolor{gray}{1\cdot}x_4 + \textcolor{gray}{1\cdot}x_5 + \textcolor{gray}{0\cdot}(x_4x_5) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_2 + \textcolor{gray}{0\cdot}x_2 + \textcolor{gray}{1\cdot}(x_2x_2) \textcolor{gray}{-1\cdot}x_5 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_3 + \textcolor{gray}{0\cdot}x_3 + \textcolor{gray}{1\cdot}(x_3x_3) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{q_l(X)}w_l(X) + \textcolor{gray}{q_r(X)}w_r(X) + \textcolor{gray}{q_m(X)}w_l(X)w_r(X) + \textcolor{gray}{q_o(X)}w_o(X) + \textcolor{gray}{q_c}(X) = 0
- Gate constraints done! What about copy constraints?
\begin{bmatrix}
\textcolor{orange}{a_1} \\
\textcolor{green}{a_2} \\
\textcolor{violet}{a_3}
\end{bmatrix}
\begin{bmatrix}
\textcolor{green}{b_1} \\
\textcolor{violet}{b_2} \\
\textcolor{orange}{b_3}
\end{bmatrix}
(\textcolor{orange}{a_1} + 1\beta)\cdot(\textcolor{green}{a_2} + 2\beta)\cdot(\textcolor{violet}{a_2} + 3\beta)
\ =
(\textcolor{green}{b_1} + 2\beta) \cdot
(\textcolor{violet}{b_2} + 3\beta) \cdot
(\textcolor{orange}{b_3} + 1\beta)
Recap: Polynomials
- How do we prove the correctness of a set of equations?
\textcolor{gray}{0\cdot} x_1 + \textcolor{gray}{0\cdot}x_1 + \textcolor{gray}{1\cdot}(x_1x_1) \textcolor{gray}{-1\cdot}x_4 + \textcolor{gray}{0} = 0
\textcolor{gray}{1\cdot}x_4 + \textcolor{gray}{1\cdot}x_5 + \textcolor{gray}{0\cdot}(x_4x_5) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_2 + \textcolor{gray}{0\cdot}x_2 + \textcolor{gray}{1\cdot}(x_2x_2) \textcolor{gray}{-1\cdot}x_5 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_3 + \textcolor{gray}{0\cdot}x_3 + \textcolor{gray}{1\cdot}(x_3x_3) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{q_l(X)}w_l(X) + \textcolor{gray}{q_r(X)}w_r(X) + \textcolor{gray}{q_m(X)}w_l(X)w_r(X) + \textcolor{gray}{q_o(X)}w_o(X) + \textcolor{gray}{q_c}(X) = 0
- Gate constraints done! What about copy constraints?
\begin{bmatrix}
\textcolor{orange}{a_1} \\
\textcolor{green}{a_2} \\
\textcolor{violet}{a_3}
\end{bmatrix}
\begin{bmatrix}
\textcolor{green}{b_1} \\
\textcolor{violet}{b_2} \\
\textcolor{orange}{b_3}
\end{bmatrix}
(\textcolor{orange}{a_1} + 1\beta)\cdot(\textcolor{green}{a_2} + 2\beta)\cdot(\textcolor{violet}{a_2} + 3\beta)
\ =
(\textcolor{green}{b_1} + 2\beta) \cdot
(\textcolor{violet}{b_2} + 3\beta) \cdot
(\textcolor{orange}{b_3} + 1\beta)
Recap: Polynomials
- How do we prove the correctness of a set of equations?
\textcolor{gray}{0\cdot} x_1 + \textcolor{gray}{0\cdot}x_1 + \textcolor{gray}{1\cdot}(x_1x_1) \textcolor{gray}{-1\cdot}x_4 + \textcolor{gray}{0} = 0
\textcolor{gray}{1\cdot}x_4 + \textcolor{gray}{1\cdot}x_5 + \textcolor{gray}{0\cdot}(x_4x_5) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_2 + \textcolor{gray}{0\cdot}x_2 + \textcolor{gray}{1\cdot}(x_2x_2) \textcolor{gray}{-1\cdot}x_5 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_3 + \textcolor{gray}{0\cdot}x_3 + \textcolor{gray}{1\cdot}(x_3x_3) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{q_l(X)}w_l(X) + \textcolor{gray}{q_r(X)}w_r(X) + \textcolor{gray}{q_m(X)}w_l(X)w_r(X) + \textcolor{gray}{q_o(X)}w_o(X) + \textcolor{gray}{q_c}(X) = 0
- Gate constraints done! What about copy constraints?
\begin{bmatrix}
\textcolor{orange}{a_1} \\
\textcolor{green}{a_2} \\
\textcolor{violet}{a_3}
\end{bmatrix}
\begin{bmatrix}
\textcolor{green}{b_1} \\
\textcolor{violet}{b_2} \\
\textcolor{orange}{b_3}
\end{bmatrix}
(\textcolor{orange}{a_1} + 1\beta + \gamma)\cdot(\textcolor{green}{a_2} + 2\beta + \gamma)\cdot(\textcolor{violet}{a_2} + 3\beta + \gamma)
\ =
(\textcolor{green}{b_1} + 2\beta + \gamma) \cdot
(\textcolor{violet}{b_2} + 3\beta + \gamma) \cdot
(\textcolor{orange}{b_3} + 1\beta + \gamma)
Recap: Polynomials


\pi
Proof
Back to Constraints
\textcolor{gray}{2.} a_1
\textcolor{gray}{+3.}b_1
\textcolor{gray}{+1.}c_1
\textcolor{gray}{-1.}d_1
\textcolor{gray}{+5} = 0
\textcolor{gray}{0.} a_3
\textcolor{gray}{+0.}b_3
\textcolor{gray}{+1.}a_3b_3
\textcolor{gray}{-1.}c_3
\textcolor{gray}{+0} = 0
(a_i,b_i) \ \textcolor{grey}{+_{\text{ecc}}} \ (c_i, d_i) = (a_{i+1},b_{i+1})
\textsf{ecc gate}:
\underbrace{\hspace{2cm}}
StandardPlonk
\underbrace{\hspace{1cm}}
TurboPlonk
\textsf{a}
\textsf{b}
\textsf{c}
\textsf{d}
i
1
a_1
b_1
c_1
d_1
2
a_2
b_2
c_2
d_2
3
a_3
b_3
c_3
d_3
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
i
a_{i}
b_{i}
c_{i}
d_{i}
i+1
a_{i+1}
b_{i+1}
c_{i+1}
d_{i+1}
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
n-1
a_{n-1}
b_{n-1}
c_{n-1}
d_{n-1}
n
a_{n}
b_{n}
c_{n}
d_{n}
\textsf{add gate}:
\textsf{mult gate}:
Width = \(4\)
Circuit size = \(n\)
c_1 = a_i,
d_2 = b_i,
a_{i+1} = c_{n-1},
b_{i+1} = d_{n-1},
\underbrace{\hspace{1cm}}
Copy constraints
Cell-wise permutation
Plookup
\textsf{a}
\textsf{b}
\textsf{c}
\textsf{d}
i
1
a_1
b_1
c_1
d_1
2
a_2
b_2
c_2
d_2
3
a_3
b_3
c_3
d_3
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
i
a_{i}
b_{i}
c_{i}
d_{i}
i+1
a_{i+1}
b_{i+1}
c_{i+1}
d_{i+1}
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
n-1
a_{n-1}
b_{n-1}
c_{n-1}
d_{n-1}
n
a_{n}
b_{n}
c_{n}
d_{n}
Width = \(4\)
Circuit size = \(n\)
\textsf{key}_1
\textsf{key}_2
\textsf{key}_3
\textsf{val}
t_1^{(1)}
t_1^{(2)}
t_1^{(3)}
v_1
t_2^{(1)}
t_2^{(2)}
t_2^{(3)}
v_2
t_3^{(1)}
t_3^{(2)}
t_3^{(3)}
v_3
t_l^{(1)}
t_l^{(2)}
t_l^{(3)}
v_l
Lookup Table \(T\)
Lookup table size = \(l\)
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
Lookup argument:
(a_i,b_i,c_i,d_i) \in T
\underbrace{\hspace{8.5cm}}
PLookup
Wait, Why Plookup?
- Lets take a peek into the SHA-256 internals


XOR
AND
Right-rotate
Shift-right
- Tons of bitwise operations! Very fast on CPUs!


Solutions?
- We can avoid using heavy bitwise operations:
- Use hash functions which don't have bitwise operations
- SNARK-friendly hash functions: Poseidon, Rescue
- But they are yet to the undergo the test-of-time and test-of-Ariel!
- Figure out how to do bitwise operations efficiently
- I believe this is what led to creation of Plookup!
- We can have lookup tables for AND, XOR, ROTR, etc.
- Further, we can have fixed-base scalar multiplication in lookup tables!
- Sounds too good to be true?
- The tradeoff in using lookup tables is the total lookup table size \(L\)
\textsf{Prover} \approx \mathcal{O}(\text{max}(n, L))
Example
- Suppose we wish to compute bitwise XOR in the circuit
- Here \((a,b,c)\) are 11-bit integers
- Lookup table \(T\) must have all possible solutions:
a \oplus b = c
Credit: Ariel's talk titled Plookup in Action.
a
b
c
00000000000
00000000000
00000000000
00000000000
00000000001
00000000001
00000000000
00000000010
00000000010
\vdots
\vdots
\vdots
- But here \(|T|=2^{22}\), that's too large!
Example (Continued)
- Lets say we need 2-bit XOR: naively \(|T| = 2^{4} =16\)
- Another table \(T'\) which contains only two columns: \((a, a_s)\)
- Here, \(a_s\) is the sparse form of \(a\)
- Say \(a=01\) and \(b=11\)
- Look up the sparse forms of \(a,b\) from \(T'\)
Credit: Ariel's talk titled Plookup in Action.
c_s = a_s + b_s
=
\textcolor{darkred}{0}0\textcolor{darkred}{0}1 +
\textcolor{darkred}{0}1\textcolor{darkred}{0}1 = 1 + 5 = 6 =
\textcolor{darkred}{0}1\textcolor{darkred}{1}0
c = \text{recover}(c_s) = 10
- Lookup operation + field addition operation
- In the previous eg, \(|T|=2^{22}\) and sparse form compresses that to \(|T'|=2^{10}\)
a
a_s
00
\textcolor{darkred}{0}0\textcolor{darkred}{0}0
01
10
11
\textcolor{darkred}{0}0\textcolor{darkred}{0}1
\textcolor{darkred}{0}1\textcolor{darkred}{0}0
\textcolor{darkred}{0}1\textcolor{darkred}{0}1
\textsf{val}
0
1
4
5
Summary
- We tried to understand the how following parts of Plonk work
- Gate constraints
- Copy constraints
- Custom constraints (TurboPlonk)
- Lookup constraints (UltraPlonk)
- We'll be halting the study clubs for a bit from next week.